Một vật dao động điều hòa dọc theo trục Ox, có đồ thị biểu diễn sự phụ thuộc của bình phương vận tốc \(\left( {{v^2}} \right)\) vào li độ x như hình vẽ. Tần số góc của vật là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương trình dao động điều hòa và phương trình vận tốc:
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{x = A.\cos \left( {\omega t + \varphi } \right)}\\{v = - \omega A.\sin \left( {\omega t + \varphi } \right) \\\Rightarrow {v^2} = {\omega ^2}.{A^2}.{{\sin }^2}\left( {\omega t + \varphi } \right)}\end{array}} \right.}\\{ \Rightarrow {v^2} = {\omega ^2}.\left( {{A^2} - {x^2}} \right)}\end{array}\)
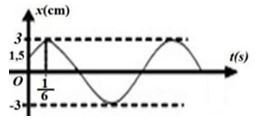
Từ đồ thị, ta thấy biên độ A = 2cm và tại \(x = 0;{v^2} = 0,04\)
Vậy ta có : \({v^2} = {\omega ^2}.{A^2} = 0,04 \\\Rightarrow \omega = \sqrt {\frac{{{v^2}}}{{{A^2}}}} = \sqrt {\frac{{0,04}}{{0,{{02}^2}}}} = 10\left( {rad/s} \right)\)
Chọn A.
Đề thi giữa HK1 môn Vật Lý 12 năm 2022-2023
Trường THPT Nguyễn Duy Hiệu
.JPG)
.JPG)