Đề thi HK1 môn Toán 7 KNTT năm 2022-2023
Trường THCS Tân Phong
-
Câu 1:
Trong các phân số sau, phân số nào biểu diễn số hữu tỉ \( - 0,125?\)
A. \(\dfrac{1}{8}\)
B. \( - \dfrac{1}{8}\)
C. \( - \dfrac{1}{{125}}\)
D. \(\dfrac{1}{{125}}\)
-
Câu 2:
Kết quả của phép tính: \({\left( { - 0,08} \right)^4}{.10^4}\) là:
A. \(0,{8^4}\)
B. \({8^4}\)
C. \({10.8^4}\)
D. \(0,{08^4}\)
-
Câu 3:
So sánh \(2 + \sqrt {37} \) và \(6 + \sqrt 2 \)?
A. \(2 + \sqrt {37} > 6 + \sqrt 2 \)
B. \(2 + \sqrt {37} < 6 + \sqrt 2 \)
C. \(2 + \sqrt {37} = 6 + \sqrt 2 \)
D. Không có đáp án
-
Câu 4:
Sắp xếp các số \(\left| { - 3} \right|\,\,;\,\,\sqrt 6 \,\,;\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \,\,;\,\, - \dfrac{7}{3}\) theo thứ tự tăng dần.
A. \( - \dfrac{7}{3}\,\,;\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt 6 \,\,;\,\,\left| { - 3} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \)
B. \( - \dfrac{7}{3}\,\,;\,\,\sqrt 6 \,;\,\,\left| { - 3} \right|\,\,\,;\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \)
C. \(\,\sqrt {\dfrac{{128}}{2}} \,\,;\,\,\,\left| { - 3} \right|\,\,;\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\,\sqrt 6 \,\,;\,\, - \dfrac{7}{3}\,\,\)
D. \( - \dfrac{7}{3}\,\,\,;\,\,\sqrt 6 \,\,;\,\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \,\,;\,\,\,\left| { - 3} \right|\)
-
Câu 5:
Cho góc bẹt \(xOy\). Vẽ tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\). Vẽ tia \(Om\) là phân giác của góc \(xOz\). Vẽ tia \(On\) là tia phân giác của góc \(zOy\). Tính số đo góc \(mOn?\)
A. \(\angle mOn = {30^0}\)
B. \(\angle mOn = {60^0}\)
C. \(\angle mOn = {90^0}\)
D. \(\angle mOn = {120^0}\)
-
Câu 6:
Tính số đo của góc \(x\) trong hình vẽ dưới đây:
.png)
A. \(x = {85^0}\)
B. \(x = {110^0}\)
C. \(x = {115^0}\)
D. \(x = {95^0}\)
-
Câu 7:
Cho \(\Delta ABC = \Delta DEF.\) Biết \(\angle A = {33^0}\). Khi đó:
A. \(\angle D = {33^0}\)
B. \(\angle D = {42^0}\)
C. \(\angle E = {32^0}\)
D. \(\angle D = {66^0}\)
-
Câu 8:
Số tam giác cân trong hình vẽ dưới đây là:
.png)
A. \(2\)
B. \(1\)
C. \(4\)
D. \(3\)
-
Câu 9:
Đường trung trực của đoạn thẳng \(AB\) là đường thẳng …
A. song song với đoạn thẳng \(AB\).
B. vuông góc với đoạn thẳng \(AB\).
C. đi qua trung điểm của đoạn thẳng \(AB\).
D. vuông góc với đoạn thẳng \(AB\) tại trung điểm của nó.
-
Câu 10:
Đâu không phải là số thập phân vô hạn tuần hoàn?
A. 2,47123123…;
B. 3,101001000…;
C. 5,33333…;
D. 7,21212….
-
Câu 11:
Các số hữu tỉ \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\) được sắp xếp theo thứ tự tăng dần là:
A. \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{{18}}{{13}}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{3}{5}.\)
B. \(\frac{{ - 5}}{9}\,\,;\,\,\frac{{ - 5}}{{11}}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\,\,;\frac{7}{5}.\)
C. \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\,\,;\,\,\frac{7}{5}.\)
D. \(\frac{{ - 5}}{9}\,\,;\,\,\frac{{ - 5}}{{11}}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{{18}}{{13}}.\)
-
Câu 12:
Kết quả của phép tính: \(\frac{{{3^{10}}}}{{{5^{10}}}}{.5^{10}}\) là:
A. \({3^5}\)
B. \({3^{20}}\)
C. \({3^{10}}\)
D. \({5.3^{10}}\)
-
Câu 13:
Kết quả của phép tính: \(\sqrt {0,04} + \sqrt {0,25} + 2,31\) là:
A. \(2,53\)
B. \(2,96\)
C. \(2,6\)
D. \(3,01\)
-
Câu 14:
Cho \(x,y\) là hai số thực tùy ý. Khẳng định nào sau đây đúng?
A. \(\left| {x - y} \right| = x - y\)
B. \(\left| {x - y} \right| = \left| x \right| - \left| y \right|\)
C. \(\left| {x + y} \right| = \left| x \right| + \left| y \right|\)
D. \(\left| {x + y} \right| = \left| x \right| - \left| y \right|\) nếu \(x > 0 > y\) và \(\left| x \right| \ge \left| y \right|\)
-
Câu 15:
Quan sát hình vẽ bên dưới:
Tính số đo góc \(xOz\), biết \(\frac{1}{5}\angle xOz = \frac{1}{4}\angle yOz\).
A. \(\angle xOz = {40^0}\)
B. \(\angle xOz = {50^0}\)
C. \(\angle xOz = {30^0}\)\(\)
D. \(\angle xOz = {60^0}\)
-
Câu 16:
Tìm số đo của \(x\) trong hình vẽ dưới đây?
.jpg)
A. \(x = {55^0}\)
B. \(x = {75^0}\)
C. \(x = {60^0}\)
D. \(x = {70^0}\)
-
Câu 17:
Cho hai tam giác \(ABC\) và \(MNP\) có \(\angle ABC = \angle MNP,\angle ACB = \angle MPN\). Cần thêm một điều kiện để tam giác \(ABC\) và tam giác \(MNP\) bằng nhau theo trường hợp góc – cạnh – góc là:
A. \(AC = MP\)
B. \(AB = MN\)
C. \(BC = NP\)
D. \(AC = MN\)
-
Câu 18:
Quan sát hình vẽ bên dưới, tính số đo góc \(\angle ABH\) biết \(a//b\).
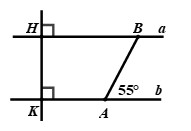
A. \(\angle ABH = {125^0}\)
B. \(\angle ABH = {65^0}\)
C. \(\angle ABH = {55^0}\)
D. \(\angle ABH = {95^0}\)
-
Câu 19:
Tìm chữ số thập phân thứ sáu của số thập phân 4,4(62)?
A. 2
B. 4
C. 6
D. 5
-
Câu 20:
Biểu đồ đoạn thẳng trên cho biết nhiệt độ ở Hà Nội trong ngày 07/05/2021 tại một số thời điểm. Hãy cho biết thời điểm nào nhiệt độ thấp nhất, cao nhất?
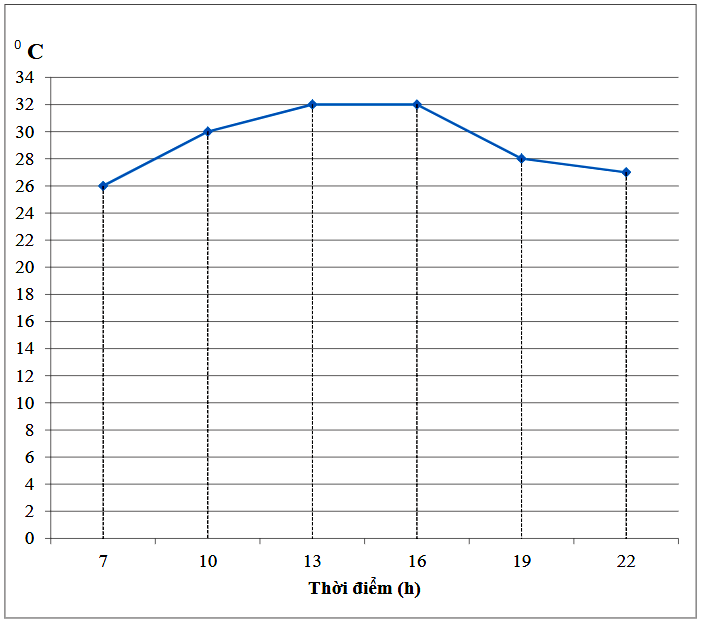
A. Thời điểm nhiệt độ thấp nhất là 26 độ C; thời điểm nhiệt độ cao nhất là 32 độ C.
B. Thời điểm nhiệt độ thấp nhất là 22 độ C; thời điểm nhiệt độ cao nhất là 32 độ C
C. Thời điểm nhiệt độ thấp nhất là 22 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
D. Thời điểm nhiệt độ thấp nhất là 7 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
-
Câu 21:
Số \(\dfrac{{ - 4}}{{ - 5}}\) được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
A.
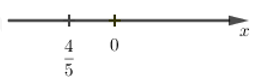
B.
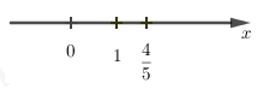
C.
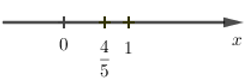
D.
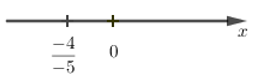
-
Câu 22:
Số hữu tỉ x thoả mãn \(x - \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right) = \dfrac{9}{{20}}\) là:
A. \(\dfrac{5}{2}\)
B. \(\dfrac{3}{{10}}\)
C. \(\dfrac{7}{6}\)
D. \(\dfrac{{ - 5}}{{17}}\)
-
Câu 23:
Kết quả của phép tính: \(\dfrac{1}{2} + {\left[ {{{\left( { - 1103} \right)}^{1999}}} \right]^0}\) là:
A. \(\dfrac{1}{2}\)
B. \(1\dfrac{1}{2}\)
C. \(1\)
D. \(\dfrac{{ - 1}}{2}\)
-
Câu 24:
Số nào dưới đây là số vô tỉ?
A. \(\sqrt 7 \)
B. \(1,\left( {01} \right)\)
C. \(\sqrt {16} \)
D. \(\dfrac{{ - 1}}{7}\)
-
Câu 25:
Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thể giới. Để xây dựng được công trình này, người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 52 198,16 \({m^2}\). (Theo khoahoc.tv)
Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất).
A. \(229,5m\)
B. \(229m\)
C. \(228,5m\)
D. \(228m\)
-
Câu 26:
Kết quả của phép tính: \(\left| {5 - \sqrt {45} } \right| + 15 - \sqrt {45} \) là:
A. \(10\)
B. \(20 - 2\sqrt {45} \)
C. \(20\)
D. \(10 - \sqrt {45} \)
-
Câu 27:
Tính số đo của góc \(x,y\) trong hình vẽ dưới đây:
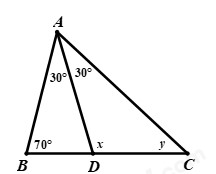
A. \(x = {120^0},y = {30^0}\)
B. \(x = {115^0},y = {35^0}\)
C. \(x = {100^0},y = {50^0}\)
D. \(x = {105^0},y = {45^0}\)
-
Câu 28:
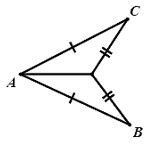
Quan sát hình vẽ sau:
Tính số đo của góc \(B\), biết \(\angle ACD = {30^0}\).
A. \({30^0}\)
B. \({60^0}\)
C. \({25^0}\)
D. \({40^0}\)
-
Câu 29:
Cho tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM,\angle B = \angle P = {90^0}\). Cần thêm một điều kiện gì để tam giác \(ABC\) và tam giác \(NPM\) bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông?
A. \(AB = PM\)
B. \(AB = PN\)
C. \(AC = MN\)
D. \(\angle A = \angle N\)
-
Câu 30:
Tỉ lệ phần trăm số học sinh xuất sắc, giỏi, khá, trung bình của một lớp được biểu diễn qua biểu đồ hình quạt tròn sau:
.png)
Tìm tỉ số phần trăm số học sinh xuất sắc và số hóc inh giỏi của lớp đó, biết rằng số học sinh xuất sắc bằng số học sinh giỏi.
A. Số học sinh xuất sắc chiếm \(14\% \), số học sinh giỏi chiếm \(14\% \).
B. Số học sinh xuất sắc chiếm \(16\% \), số học sinh giỏi chiếm \(16\% \).
C. Số học sinh xuất sắc chiếm \(15\% \), số học sinh giỏi chiếm \(15\% \).
D. Số học sinh xuất sắc chiếm \(12\% \), số học sinh giỏi chiếm \(12\% \).
-
Câu 31:
Phát biểu nào sau đây là sai?
A. Mọi số vô tỉ đều là số thực.
B. Mọi số thực đều là số vô tỉ.
C. Số 0 là số hữu tỉ.
D. \( - \sqrt 2 \) là số vô tỉ.
-
Câu 32:
Một tam giác có độ dài cạnh \(\frac{2}{9}m\) và chiều cao ứng với cạnh đó bằng nửa cạnh đó. Tính diện tích của tam giác đã cho.
A. \(\frac{1}{9}{m^2}\)
B. \(\frac{1}{{18}}{m^2}\)
C. \(\frac{2}{{81}}{m^2}\)
D. \(\frac{1}{{81}}{m^2}\)
-
Câu 33:
Kết quả của phép tính: \(\left| {6 - \sqrt {34} } \right| + 3 + \sqrt {34} \) là:
A. \(9 + 2\sqrt {34} \)
B. \(3 + 2\sqrt {34} \)
C. \(9\)
D. \(3\)
-
Câu 34:
Cho biết \(1inch \approx 2,54cm\). Tính độ dài đường chéo bằng đơn vị một màn hình \(36inch\) và làm tròn đến hàng phần mười.
A. \(91,54\,cm\)
B. \(91,5\,cm\)
C. \(91,44\,cm\)
D. \(91,4\,cm\)
-
Câu 35:
Cho tam giác ABC có \(\widehat A = {98^0},\widehat C = {52^0}\). Số đo góc B là:
A. \({30^0}\)
B. \({35^0}\)
C. \({60^0}\)
D. \({90^0}\)
-
Câu 36:
Một tam giác cân có góc ở đỉnh bằng \({52^0}\) thì số đo góc ở đáy là:
A. \({54^0}\)
B. \({64^0}\)
C. \({72^0}\)
D. \({90^0}\)
-
Câu 37:
Ở hình vẽ bên dưới có \(AB\) và \(CD\) cắt nhau tại \(O,Ot\) là tia phân giác của góc \(BOC\)\(,\angle AOC - \angle BOC = {68^0}\). Số đo góc \(BOt\) là:
A. \({56^0}\)
B. \({62^0}\)
C. \({28^0}\)
D. \({23^0}\)
-
Câu 38:
Cho hình vẽ bên dưới, biết hai đường thẳng \(m\) và \(n\) song song với nhau. Tính số đo góc \({B_4}?\)
A. \({80^0}\)
B. \({100^0}\)
C. \({120^0}\)
D. \({140^0}\)
-
Câu 39:
Biểu đồ hình quạt tròn dùng để:
A. So sánh số liệu của hai đối tượng cùng loại.
B. So sánh các thành phần trong toàn bộ dữ liệu.
C. Biểu diễn sự thay đổi của một đại lượng theo thời gian.
D. Biểu diễn sự chênh lệch số liệu giữa các đối tượng.
-
Câu 40:
Biểu đồ bên dưới biểu diễn thu nhập bình quân dầu người/năm của Việt Nam (tính theo đô la Mỹ) ở một số năm trong những gia đoạn từ 1986 đến 2020. Hãy cho biết năm nào Việt Nam có thu nhập cao nhất, cụ thể là bao nhiêu đô la?
.png)
A. Năm 1991, Việt Nam có mức thu nhập thấp nhất là 138 đô la/năm.
B. Năm 2019, Việt Nam có mức thu nhập cao nhất là 2738 đô la/năm.
C. Năm 2018, Việt Nam có mức thu nhập cao nhất là 2566 đô la/năm.
D. Năm 2020, Việt Nam có mức thu nhập cao nhất là 2786 đô la/năm.
.JPG)
.JPG)
.JPG)











