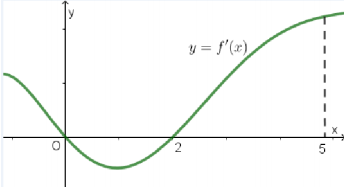
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y=f'(x) như hình vẽ bên. Tính số điểm cực trị của hàm số
\(y=f\left(x^{2}\right)\) trên khoảng \((-\sqrt{5} ; \sqrt{5})\)
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiXét hàm số \(g(x)=f\left(x^{2}\right) \Rightarrow g^{\prime}(x)=2 x f^{\prime}\left(x^{2}\right)\) .
\(g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l} x=0 \\ f^{\prime}\left(x^{2}\right)=0 \end{array} \Leftrightarrow\left[\begin{array}{l} x=0 \\ x^{2}=0 \\ x^{2}=2 \end{array} \Leftrightarrow\left[\begin{array}{l} x=0 \\ x=\pm \sqrt{2} \end{array}\right.\right.\right.\)
Ta có bảng xét dấu:
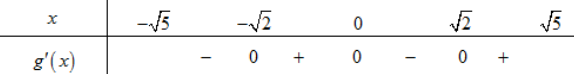
Từ đó suy ra hàm số \(y=f\left(x^{2}\right)\) có 3 điểm cực trị.
ADMICRO
YOMEDIA
ZUNIA9
.jpg.png)











