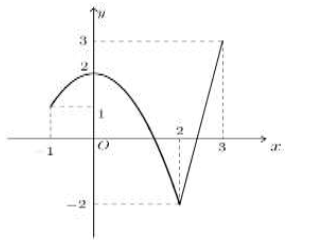
Cho hàm số \(y = f\left( x \right)\) liên tục, có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây:

Ký hiệu \(g\left( x \right) = f\left( {2\sqrt {2x} + \sqrt {1 – x} } \right) + m.\) Tìm điều kiện của tham số m sao cho \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) > 2\mathop {\min }\limits_{\left[ {0;1} \right]} g\left( x \right).\)

Câu hỏi liên quan

• \(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - x - 9}}{{x + 3}}\text{ trên đoạn } \left[ { - 5; - 4} \right]\)

• Cho hàm số \(y=\sqrt{x+1}-\sqrt{x-2}\) . Khẳng định nào sau đây sai ?

• Hàm số \(y=\sqrt{x^{2}+1}+x^{2}\) có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1;1] lần lượt là:

ZUNIA12

• Giá trị lớn nhất của hàm số \(y=\frac{x+\sqrt{1+9 x^{2}}}{8 x^{2}+1}\) trên khoảng \((0 ;+\infty)\) là:

• Giá trị lớn nhất của hàm số \(y=2 \sin x-\frac{4}{3} \sin ^{3} x \text { trên }[0 ; \pi]\) là:

• Để giá trị lớn nhất của hàm số \(y = \left| {\sqrt {2x – {x^2}} – 3m + 4} \right|\) đạt giá trị nhỏ nhất thì m thỏa

• Giá trị nhỏ nhất của hàm số \(y=x^{3}-3 x+5\) trên đoạn [0;2] là:

• Giá trị lớn nhất, nhỏ nhất của hàm số \(y=\frac{2 x^{2}+3 x+3}{x+1}\) trên đoạn [0;2] lần lượt là:

• Tìm m để bất phương trình x²-5mx+9 ≥ 0 có nghiệm x ?

• Cho hàm số f(x) lên tục trên đoạn [-1; 3] và có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số \(y=f\left(3 \sin ^{2} x-1\right)\) bằng
  

• Một hành lang giữa hai tòa tháp có hình dạng một hình lăng trụ đứng. Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20m, rộng 5m. Với độ dài xấp xỉ nào của BC thì thể tích hành lang này lớn nhất

  

• Giá trị nhỏ nhất của hàm số y = x + e^2x trên đoạn [0;2] là

• \(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{11x - 1}}{{2x + 3}}\text{ trên đoạn } \left[ {2;6} \right]\)

• Tìm giá trị nhỏ nhất của hàm số \(y=(2 \sin x+1)^{2}+2 \text { trên đoạn }\left[-\frac{\pi}{2} ; \frac{\pi}{2}\right]\)

• Giá trị nhỏ nhất của hàm số \(y=e^{x}\left(x^{2}-3\right)\) trên đoạn [-2;2]

• Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=\sqrt{x-1}+\sqrt{7-x} .\) . Khi đó
  có bao nhiêu số nguyên dương nằm giữa m và M ? 

• GTNN của các hàm số sau: \(y=-x^{3}+3 x+1\) trên \([0 ;+\infty)\) là 
   

• Giá trị lớn nhất của hàm số \(y = {\cos ^4}x – {\cos ^2}x + 4\) bằng:

• Hàm số \(y=x^{4}-2 x^{2}+1\) có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [0 ; 2] lần lượt là:

• Hàm số \(y=x^{2}+2 x+1\) có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [0;1] lần lượt là \(y_{1} ; y_{2}\) Khi đó tích \(y_{1} . y_{2}\)  bằng: