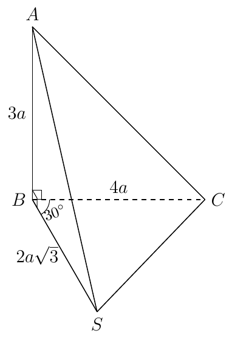
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a và AB ⊥ (SBC) . Biết SB = \(2a\sqrt 3 \) và \(\widehat {SBC} = {30^0}\). Thể tích khối chóp S.ABC bằng:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTa có:
\({S_{SBC}} = \frac{1}{2}BC.BS.\sin \widehat {SBC} = \frac{1}{2}.4a.2a\sqrt 3 \sin {30^0} = 2{a^2}\sqrt 3 \)
Thể tích của khối chóp S.ABC là:
\({V_{S.ABC}} = \frac{1}{3}AB.{S_{SBC}} = \frac{1}{3}3a.2{a^2}\sqrt 3 = 2{a^3}\sqrt 3 \)
ADMICRO
YOMEDIA
ZUNIA9