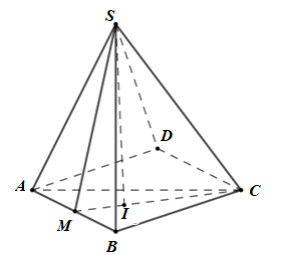
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, AB = 2a, AD = a (a > 0). M là trung điểm của AB, tam giác SMC vuông tại S, (SMC) vuông góc (ABCD), SM tạo với đáy góc 600. Thể tích của khối chóp S.ABCD là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTrong (SMC) kẻ SI⊥MC(I∈MC) ta có:
\(\left\{ \begin{array}{l} (SMC) \bot (ABCD) = MC\\ SI \subset (SMC),SI \bot MC \end{array} \right. \Rightarrow SI \bot (ABCD)\)
⇒ IM là hình chiếu của SM lên (ABCD)
\( \Rightarrow \angle \left( {SM;\left( {ABCD} \right)} \right) = \angle \left( {SM;IM} \right) = \angle SMI = \angle SMC = {60^0}\)
Áp dụng định lí Pytago trong tam giác BMC vuông tại B :
\(BM = \frac{{AB}}{2} = a;{\mkern 1mu} {\mkern 1mu} BC = a \Rightarrow MC = \sqrt {B{C^2} + B{M^2}} = a\sqrt 2 \)
Xét tam giác SMC vuông tại S có \( \angle SMC = {60^0};{\mkern 1mu} {\mkern 1mu} MC = a\sqrt 2 \Rightarrow SM = MC.\cos {60^0} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác SMI vuông tại I có \( \angle SMI = {60^0};{\mkern 1mu} {\mkern 1mu} SM = \frac{{a\sqrt 2 }}{2} \Rightarrow SI = SM.sin{60^0} = \frac{{a\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 6 }}{4}\)
Vậy thể tích khối chóp là \( V = \frac{1}{3}SI.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 6 }}{4}.2{a^2} = \frac{{{a^3}\sqrt 6 }}{6}.\)
Đáp án cần chọn là: A