Cho tứ diện ABCD có ba mặt (ABC, ACD, ADB ) là ba tam giác bằng nhau và cân tại định A. Số mặt phẳng đối xứng của tứ diện đó là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có: Ba mặt ABC,ACD,ADB là ba tam giác bằng nhau và cân tại định A
\(\to \left\{ \begin{array}{l} AB = AC = AD\\ BC = CD = BD \end{array} \right.\)
TH1: Ta có: \(\left\{ \begin{array}{l} AB = AC = AD\\ BC = CD = BD \end{array} \right.\) và các cạnh bên không bằng các cạnh đáy
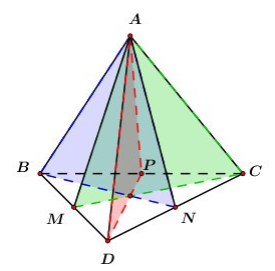
Khi đó ta có các mặt phẳng đối xứng là: (ABN),(ACM),(ADP) với M,N,P lần lượt là trung điểm của các cạnh BD,DC,BC.
TH2: Ta có: \(\left\{ \begin{array}{l} AB = AC = AD\\ BC = CD = BD \end{array} \right.\) và các cạnh bên bằng các cạnh đáy
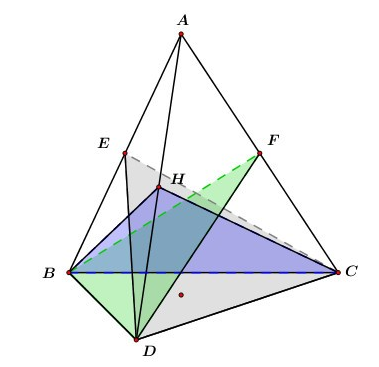
Khi đó ta có các mặt đối xứng như TH1 và thêm các mặt phẳng (EDC),(FBD),(HBC) với E,F,H lần lượt là trung điểm của các cạnh AB,AC,AD.
.PNG)
.PNG)
.png)











