Tìm tất cả các giá trị của \(m\) để phương trình \({{\left( 7-3\sqrt{5} \right)}^{{{x}^{2}}}}+m{{\left( 7+3\sqrt{5} \right)}^{{{x}^{2}}}}={{2}^{{{x}^{2}}-1}}\) có đúng hai nghiệm phân biệt.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPT \(\Leftrightarrow {{\left( \frac{7-3\sqrt{5}}{2} \right)}^{{{x}^{2}}}}+m{{\left( \frac{7+3\sqrt{5}}{2} \right)}^{{{x}^{2}}}}=\frac{1}{2}\).
Đặt \(t={{\left( \frac{7-3\sqrt{5}}{2} \right)}^{{{x}^{2}}}}\in \left( 0;1 \right]\). Khi đó PT \(\Rightarrow 2{{t}^{2}}-t+2m=0\Leftrightarrow 2m=t-2{{t}^{2}}=g\left( t \right)\) (1).
Ta có \({g}'\left( t \right)=1-4t=0\Leftrightarrow t=\frac{1}{4}\).
Suy ra bảng biến thiên:
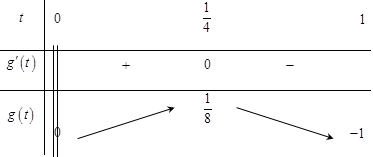
PT đã cho có đúng 2 nghiệm phân biệt \(\Leftrightarrow \) (1) có đúng 1 nghiệm \(t\in \left( 0;1 \right)\)
\( \Leftrightarrow \left[ \begin{array}{l} 2m = \frac{1}{8}\\ - 1 < 2m \le 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} m = \frac{1}{{16}}\\ - \frac{1}{2} < m \le 0 \end{array} \right.\)











