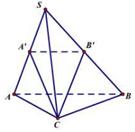
Cho hình chóp đều S.ABC có độ dài cạnh đáy là 2a, mặt bên tạo với mặt đáy một góc \({60^0}\). Tính thế tích của khối chóp S.ABC?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai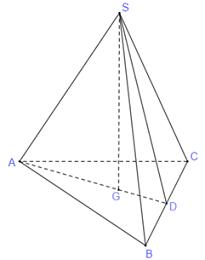
Gọi \(G\) là trọng tâm tam giác ABC, \(D\) là trung điểm BC.
S.ABC là hình chóp đều nên chân đường cao hạ từ \(S\) xuống mp đáy là trọng tâm \(G\) của đáy
Suy ra \(SG \bot \left( {ABC} \right) \Rightarrow SG \bot BC\)
Tam giác ABC là tam giác đều nên \(AD \bot BC\)
\( \Rightarrow BC \bot \left( {SAD} \right) \Rightarrow BC \bot SD\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {SBC} \right) \cap \left( {ABC} \right) = BC}\\{SD \in \left( {SBC} \right),SD \bot BC}\\{AD \in \left( {ABC} \right),AD \bot BC}\end{array}} \right. \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle SDA\).
Góc giữa mặt bên và mặt đáy bằng \({60^0}\) nên \(\angle SDA = {60^0}\).
Lại có:\(AD = \dfrac{{\sqrt 3 }}{2}BC = \sqrt 3 a \Rightarrow DG = \dfrac{1}{3}AD = \dfrac{{\sqrt 3 }}{3}a\).
\(\begin{array}{*{20}{l}}{SG = GD\tan \widehat {SDA} = \dfrac{{\sqrt 3 }}{3}a.\tan {{60}^^\circ }{\rm{\;}} = a}\\{{S_{ABC}} = \dfrac{{\sqrt 3 }}{4}.A{B^2} = \dfrac{{\sqrt 3 }}{4}.4{a^2} = \sqrt 3 {a^2}}\\{ \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SG.{S_{ABC}} = \dfrac{1}{3}.a.\sqrt 3 {a^3} = \dfrac{{\sqrt 3 }}{3}{a^3}}\end{array}\)
Chọn A.
Đề thi giữa HK1 môn Toán 12 năm 2023-2024
Trường THPT Nguyễn Thị Minh Khai