Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng \({60^0}.\) Thể tích hình chóp là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai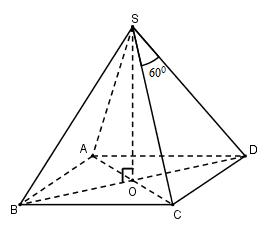
Gọi \(O = AC \cap BD\)
Vì chóp S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\)
Đặt \(SA = SB = SC = SD = a\)
Tam giác SCD có: \(SC = SD;\widehat {CSD} = {60^0} \Rightarrow \Delta SCD\) đều \( \Rightarrow CD = SC = SD = a\)
Suy ra hình vuông ABCD cạnh \(a \Rightarrow AC = BD = a\sqrt 2 \Rightarrow OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC \Rightarrow \Delta SOC\) vuông tại O
\(\Rightarrow SO = \sqrt {S{C^2} - O{C^2}} \)
\(\Rightarrow h = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\) \( \Rightarrow a = h\sqrt 2 \)
\(\Rightarrow {S_{ABCD}} = {a^2} = {\left( {h\sqrt 2 } \right)^2} = 2{h^2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}h.2{h^2} = \dfrac{{2{h^3}}}{3}\)
Đề thi giữa HK1 môn Toán 12 năm 2020
Trường THPT Chu Văn An
Câu hỏi liên quan
-
Cho các mệnh đề sau:
a. Hình chóp có đáy là hình thang thì có mặt cầu ngoại tiếp.
b. Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp.
c. Hình chóp có đáy là hình chữ nhật thì có mặt cầu ngoại tiếp.
d. Hình chóp có đáy là hình thoi thì có mặt cầu ngoại tiếp.
Số mệnh đề đúng là?
-
Thể tích khối hộp chữ nhật có diện tích đáy S và độ dài cạnh bên a là:
-
Cho hàm số \(y = \sqrt {{x^2} - 6x + 5}\). Mệnh đề nào sau đây là đúng?
-
Phương trình \({49^x} - {7^x} - 2 = 0\) có nghiệm bằng bao nhiêu?
-
Phương trình \({e^{2x}} - 3{e^x} - 4 + 12{e^{ - x}} = 0\) có các nghiệm nào?
-
Biết đường thẳng \(y = - {9 \over 4}x - {1 \over {24}}\) cắt đồ thị hàm số \(y = {{{x^3}} \over 3} + {{{x^2}} \over 2} - 2x\) tại một điểm duy nhất, ký hiệu (x0 ; y0) là tọa độ điểm đó. Tìm y0.
-
Cho hai điểm A, B phân biệt. Tập hợp tâm những mặt cầu đi qua A và B là
-
Cho hàm số có bảng biến thiên như sau:
Mệnh đề nào sau đây là đúng?
-
Trong các kí hiệu sau, kí hiệu nào không phải của khối đa diện đều?
-
Bề mặt xung quanh của một hình trụ trải trên mặt phẳng là một hình vuông cạnh a. Thể tích của khối trụ giới hạn bởi hình trụ này bằng.
-
Cho a, b là các số dương thỏa mãn điều kiện: \({\log _{{2 \over 3}}}x = {1 \over 4}{\log _{{2 \over 3}}}a + {4 \over 7}{\log _{{2 \over 3}}}b\). Khi đó x nhận giá trị nào?
-
Trong các mệnh đề sau, mệnh đề nào sai?
-
Hàm số \(y = {\left( {4{x^2} - 1} \right)^{ - 4}}\) có tập xác định là bao nhiêu?
-
Tìm tập xác định của hàm số \(y = \log \sqrt {{x^2} - x - 12}\)
-
Đồ thị sau đây là của hàm số \(y = {x^4} - 3{x^2} - 3\). Với giá trị nào của m thì phương trình \({x^4} - 3{x^2} + m = 0\) có ba nghiệm phân biệt?
-
Gọi x1, x2 là hai nghiệm của phương trình \({\log _2}^2x - 3{\log _2}x + 2 = 0\). Giá trị biểu thức \(P = {x_1}^2 + {x_2}^2\) bằng bao nhiêu?
-
Cho hàm số y = f(x) xác định trên R\{1} và có bảng biến thiên như sau:
Mệnh đề nào sau đây đúng?
-
Trên đồ thị hàm số \(y = {{2x - 1} \over {x + 1}}\) có bao nhiêu điểm có tọa độ nguyên?
-
Thể tích của khối cầu ngoại tiếp một hình hộp chữ nhật có ba kích thước \(a,\,2a,\,2a\) bằng
-
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số \(y = {{2x - 1} \over {x + 1}}\)
