Cho 4 điểm O, M, N và P nằm trong một môi trường truyền âm. Trong đó, M và N nằm trên nửa đường thẳng xuất phát từ O, tam giác MNP là tam giác đều. Tại O, đặt một nguồn âm điểm có công suất không đổi, phát âm đẳng hướng ra môi trường. Coi môi trường không hấp thụ âm. Biết mức cường độ âm tại M và N lần lượt là 50 dB và 40 dB. Mức cường độ âm tại P là:
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai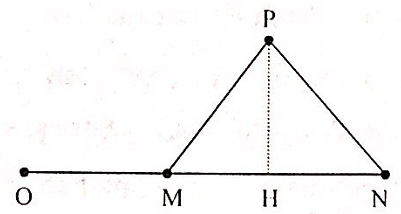
+ Ta có:
\({L_M} - {L_N} = 10\lg {\left( {\frac{{ON}}{{OM}}} \right)^2} \Rightarrow 50 - 40 = 10\lg {\left( {\frac{{ON}}{{OM}}} \right)^2} \Rightarrow \frac{{ON}}{{OM}} = {10^{1/2}}\)
+ Gọi a là cạnh tam giác đều, ta có: MN = NP = MP = a =>
\(\begin{array}{l}
\frac{{OM + a}}{{OM}} = \sqrt {10} \\
\Leftrightarrow 1 + \frac{a}{{OM}} = \sqrt {10} \Rightarrow OM = \frac{a}{{\sqrt {10} - 1}} \Rightarrow {L_P} = {L_M} + 10\lg {\left( {\frac{{OM}}{{OP}}} \right)^2}\\
{L_P} - {L_M} = 10\lg {\left( {\frac{{OM}}{{OP}}} \right)^2} \Rightarrow {L_P} = 50 + 10\lg {\left( {\frac{{OM}}{{OP}}} \right)^2}
\end{array}\)
+ Trong tam giác đều PMN ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
PH = \frac{{a\sqrt 3 }}{2}\\
MH = \frac{a}{2}
\end{array} \right. \Rightarrow OP = \sqrt {O{H^2} + P{H^2}} = 1,295a\\
\Rightarrow \frac{{OM}}{{OP}} = \frac{1}{{1,295\left( {\sqrt {10} - 1} \right)}}\\
\Rightarrow {L_P} = 50 + 10\lg {\left( {\frac{1}{{1,295\left( {\sqrt {10} - 1} \right)}}} \right)^2} = 41,1{\rm{ dB}}
\end{array}\)
Đề thi thử THPT QG năm 2021 môn Vật Lý
Trường THPT Trần Hữu Trang