Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình \(\left| f\left( {{x}^{3}}-3x \right) \right|=\frac{3}{2}\) là

Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐáp án A
Phương trình
\(\left| f\left( {{x}^{3}}-3x \right) \right|=\frac{3}{2}\\ \Leftrightarrow \left[ \begin{align} & f\left( {{x}^{3}}-3x \right)=\frac{3}{2} \\ & f\left( {{x}^{3}}-3x \right)=-\frac{3}{2} \\ \end{align} \right.\)

* Phương trình
\(f\left( {{x}^{3}}-3x \right)=\frac{3}{2}\\ \Leftrightarrow \left[ \begin{align} & {{x}^{3}}-3x={{a}_{1}},\,\left( -2<{{a}_{1}}<0 \right) \\ & {{x}^{3}}-3x={{a}_{2}},\,\left( 0<{{a}_{2}}<2 \right) \\ & {{x}^{3}}-3x={{a}_{3}},\,\left( {{a}_{3}}>2 \right) \\ \end{align} \right.\)
* Phương trình \(f\left( {{x}^{3}}-3x \right)=-\frac{3}{2}\Leftrightarrow {{x}^{3}}-3x={{a}_{4}},\,\left( {{a}_{4}}<-2 \right)\).
Đồ thị hàm số \(y={{x}^{3}}-3x\) có dạng như hình vẽ sau:
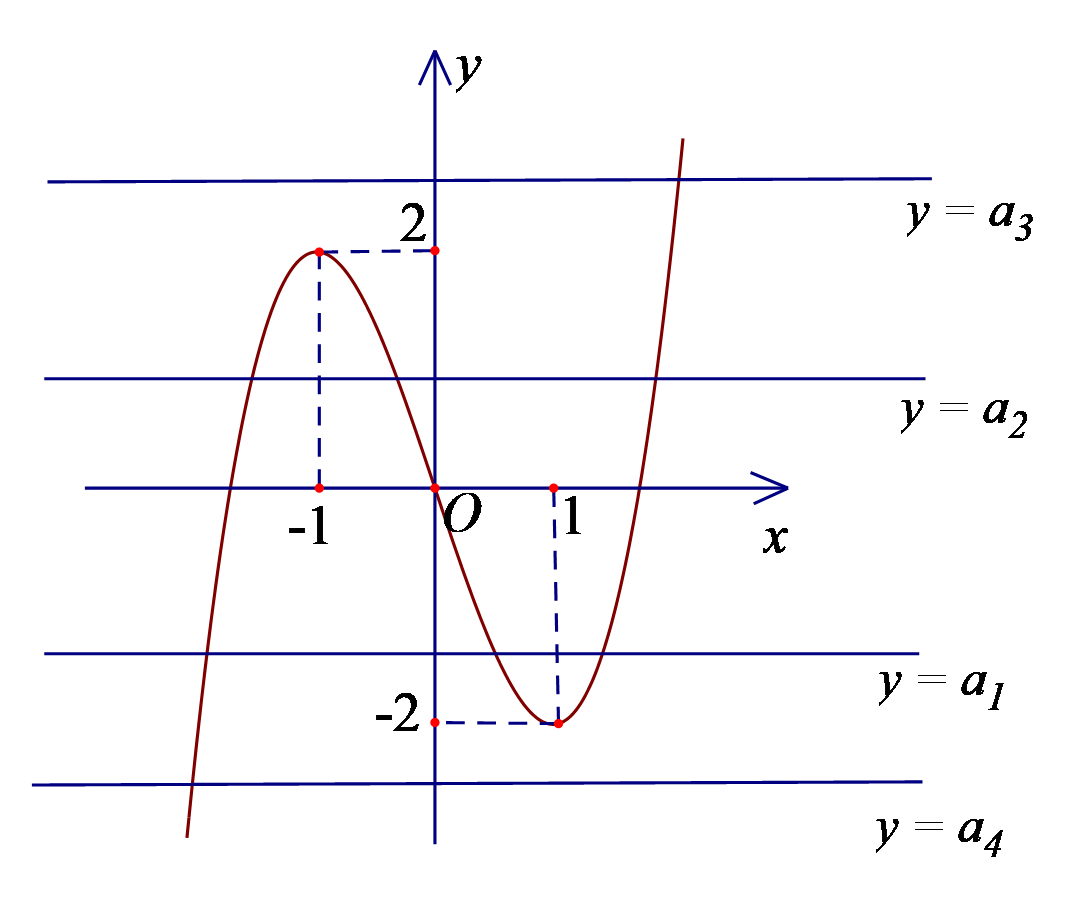
Dựa vào đồ thị trên ta có:
- Phương trình \({{x}^{3}}-3x={{a}_{1}}\) có 3 nghiệm phân biệt.
- Phương trình \({{x}^{3}}-3x={{a}_{2}}\) có 3 nghiệm phân biệt.
- Phương trình \({{x}^{3}}-3x={{a}_{3}}\) có 1 nghiệm.
- Phương trình \({{x}^{3}}-3x={{a}_{4}}\) có 1 nghiệm.
Vậy phương trình \(\left| f\left( {{x}^{3}}-3x \right) \right|=\frac{3}{2}\) có 8 nghiệm phân biệt.


















