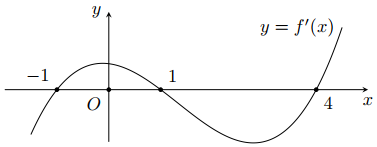
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(R,\) có bảng biến thiên như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số
\(g\left( x \right)=\left| f\left( \left| 6x-5 \right| \right)+2021+m \right|\)
Có 3 điểm cực đại?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(u\left( x \right)=\left| 6x-5 \right|,h\left( x \right)=f\left( u \right)+2021+m.\) Ta có
\(u=\sqrt{{{\left( x-1 \right)}^{2}}}\Rightarrow u'=\frac{6\left( 6x-5 \right)}{\sqrt{{{\left( 6x-5 \right)}^{2}}}}=\frac{6\left( 6x-5 \right)}{\left| 6x-5 \right|}\)
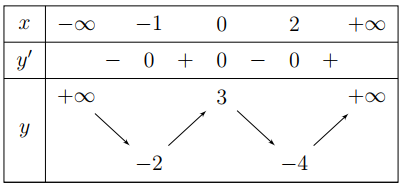
Bảng biến thiên của \(u\left( x \right):\)
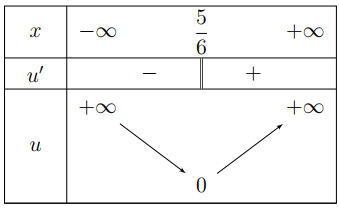
Ta có \(h'\left( x \right)=f'\left( u \right).u'\left( x \right),\)
\(h'\left( x \right)=0\Leftrightarrow \left[ \begin{align} & u=-1 \\ & u=0 \\ & u=2 \\ & x=\frac{5}{6} \\ \end{align} \right.\)
\(\Leftrightarrow \left\{ \begin{align} & x=\frac{1}{2} \\ & x=\frac{5}{6} \\ & x=\frac{7}{6} \\ \end{align} \right.\)
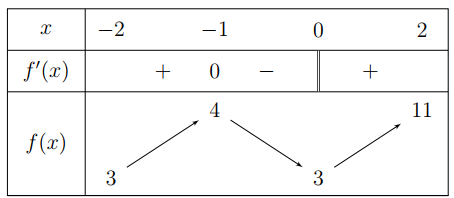
Bảng biến thiên của \(h\left( x \right):\)

Từ bảng biến thiên của \(h\left( x \right)\) ta thấy hàm số \(g\left( x \right)=\left| h\left( x \right) \right|\) có 3 điểm cực đại khi và chỉ khi
\(m+2017\)
Vì \(m\) nguyên nên \(m\in \left\{ -2023;-2022;-2021;-2020;-2019;-2018 \right\}\): có 6 giá trị
Vậy chọn đáp án B.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Sở GD&ĐT Hà Tĩnh lần 1 có đáp án

.png)
.png)