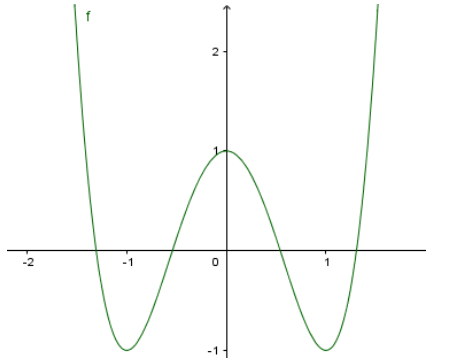
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
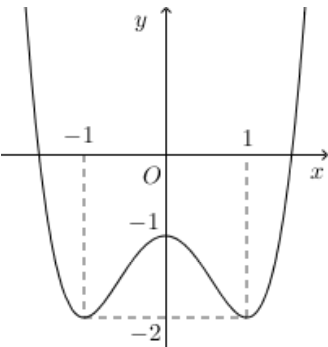
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số \(y=f(\cos x)-2 \cos x-m\) cắt trục hoành tại điểm có hoành độ thuộc khoảng \(\left(-\frac{\pi}{2} ; \frac{\pi}{2}\right)\)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương tình hoành độ giao điểm của đồ thị hàm số \(y=f(\cos x)-2 \cos x-m\) và trục hoành là:
\(f(\cos x)-2 \cos x-m=0(1)\)
Đặt \(t=\cos x, t\in(0;1]\)
Phương trình trở thành \(f(t)-2 t=m(2)\) với \(t \in(0 ; 1]\)
Bài toán trở thành tìm giá trị nguyên của m để phương trình (2) có nghiệm thuộc (0 ; 1]
Xét hàm số \(g(t)=f(t)-2 t, \text { vói } t \in(0 ; 1]\)
\(g^{\prime}(t)=f^{\prime}(t)-2\)
Nhận xét: Dựa vào đồ thị hàm số y=f(x), ta có hàm số nghịch biến trong (0 ; 1) và đạt cực trị tại x=1 nên \(f^{\prime}(x) \leq 0, \forall x \in(0 ; 1],\) suy ra \(f^{\prime}(t) \leq 0, \forall t \in(0 ; 1]\)
Do đó \(g^{\prime}(t)<0, \forall t \in(0 ; 1]\)
Bảng biến thiên g(t)
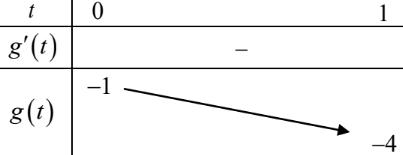
Dựa vào bảng biến thiên, suy ra phương trình (2) có nghiệm thuộc (0;1] \(\Leftrightarrow-4 \leq m<-1\).
Vì m nguyên nên\(m \in\{-4 ;-3 ;-2\} .\)
Vậy có 3 giá trị nguyên của tham số m thỏa yêu cầu bài
toán.
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Nguyễn Trãi