Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(AB = a,BC = 2a,\,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Khoảng cách giữa hai đường thẳng BD và SC bằng
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai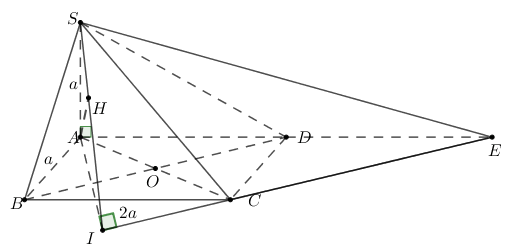
Từ C kẻ CE//BD, CE cắt AD kéo dài tại E. Khi đó ta có: \(\left( {SEC} \right) \supset SC;\left( {SEC} \right)\parallel BD\) .
Khi đó ta có: \(d\left( {BD;SC} \right) = d\left( {BD;\left( {SEC} \right)} \right) = d\left( {O;\left( {SEC} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SEC} \right)} \right)\) (do O là trung điểm của AC).
Từ A kẻ \(AI \bot CE = \left\{ I \right\}\) . Ta có: \(EC \bot AI;EC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right) \Rightarrow EC \bot \left( {SAI} \right) \Rightarrow \left( {SEC} \right) \bot \left( {SAI} \right);\left( {SEC} \right) \cap \left( {SAI} \right) = SI\) . Từ A kẻ AH vuông góc với SI. Khi đó ta có: \(d\left( {A;\left( {SEC} \right)} \right) = AH\)
Ta có:
\(\begin{array}{l}{S_{AEC}} = \frac{1}{2}CD.AE = \frac{1}{2}a.4a = 2{a^2}\\ = \frac{1}{2}.AI.EC = \frac{1}{2}.AI.BD = \frac{1}{2}AI.\sqrt {{a^2} + 4{a^2}} = \frac{1}{2}AI.a\sqrt 5 \\ \Rightarrow AI = \frac{{2.2{a^2}}}{{a\sqrt 5 }} = \frac{{4a}}{{\sqrt 5 }}\end{array}\)
Áp dụng hệ thức lượng trong tam giác vuông SAI ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{I^2}}} = \frac{1}{{{a^2}}} + \frac{5}{{16{a^2}}} = \frac{{21}}{{16{a^2}}} \Rightarrow AH = \frac{{4a}}{{\sqrt {21} }} = \frac{{4a\sqrt {21} }}{{21}}\)
Khi đó ta có: \(d\left( {BD,SC} \right) = \frac{{2a\sqrt {21} }}{{21}}\)
Chọn C.
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Trần Hưng Đạo
Câu hỏi liên quan
-
Nguyên hàm của hàm số \(f\left( x \right) = {x^4} + x\) là
-
Ông A dự định sử dụng hết \(6,7{m^2}\) kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
-
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\left( {a,b,c \in R} \right).\) Đồ thị của hàm số \(y = f\left( x \right)\) như hình vẽ bên. Số nghiệm thực của phương trình \(4f\left( x \right) - 3 = 0\) là:
-
Một người gửi tiết kiệm vào một ngân hàng với lãi suất 7,2%/ năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được (cả số tiền gửi ban đầu và lãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không rút tiền ra?
-
Cho hai hàm số \(y = f\left( x \right)\) và \(y=g\left( x \right).\) Hai hàm số \(y=f'\left( x \right)\) và \(y = g'\left( x \right)\) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right)\). Hàm số \(h\left( x \right) = f\left( {x + 7} \right) - g\left( {2x + \frac{9}{2}} \right)\) đồng biến trên khoảng nào dưới đây ?
-
Số phức có phần thực bằng 3 và phần ảo bằng 4 là:
-
Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là \(a\sqrt 3 .\) Thể tích V của khối chóp đó là bao nhiêu?
-
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
-
\(\int\limits_0^1 {{e^{3x + 1}}dx} \) bằng
-
Phương trình \(\sin \left( {3x + \frac{\pi }{3}} \right) = - \frac{{\sqrt 3 }}{2}\) có bao nhiêu nghiệm thuộc khoảng \(\left( {0;\frac{\pi }{2}} \right)\)?
-
Cho hình lập phương ABCD. A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho \(MO = \frac{1}{2}MI\) (tham khảo hình vẽ). Khi đó cosin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và \(SA = \sqrt 2 a.\) Góc giữa đường thẳng SC và mặt phẳng đáy bằng
-
Trong không gian Oxyz, cho điểm \(A\left( {2;1;3} \right)\) và đường thẳng \(d:\,\frac{{x + 1}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z - 2}}{2}.\) Đường thẳng đi qua A, vuông góc với d và cắt trục Oy có phương trình là
-
Trong không gian Oxyz, mặt phẳng đi qua điểm \(A\left( {1;2; - 2} \right)\) và vuông góc với đường thẳng \(\Delta :\frac{{x + 1}}{2} = \frac{{y - 2}}{1} = \frac{{z + 3}}{3}\) có phương trình là
-
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a,b,c,d \in R} \right)\) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
-
Cho hàm số \(y = \frac{1}{8}{x^4} - \frac{7}{4}{x^2}\) có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt \(M\left( {{x}_{1}};{{y}_{1}} \right),N\left( {{x}_{2}};{{y}_{2}} \right)\) ( M, N khác A) thỏa mãn \({y_1} - {y_2} = 3\left( {{x_1} - {x_2}} \right)?\)
-
Cho \(\int\limits_5^{21} {\frac{{dx}}{{x\sqrt {x + 4} }} = a\ln 3} + b\ln 5 + c\ln 7\) với \(a,\,b,\,c\) là các số hữu tỉ. Mệnh đề nào dưới đây đúng?
-
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + 6}}{{x + 5m}}\) nghịch biến trên khoảng \(\left( {10; + \infty } \right)\) ?
-
Trong không gian Oxyz, đường thẳng d: \(\frac{{x + 3}}{1} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 5}}{2}\) có một vecto chỉ phương là
-
\(\lim \frac{1}{{5n + 2}}\) bằng
