Cho hình chóp S .ABCD có đáy là hình thang vuông tại A và B , \(S A \perp(A B C D), A D=3 a\), \(S A=A B=B C=a\) . Gọi S ' là điểm thỏa mãn \(\overrightarrow{S S^{\prime}}=\frac{1}{2} \overrightarrow{A B}\). Tính thể tích khối đa diện \(S S^{\prime} A B C D\)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai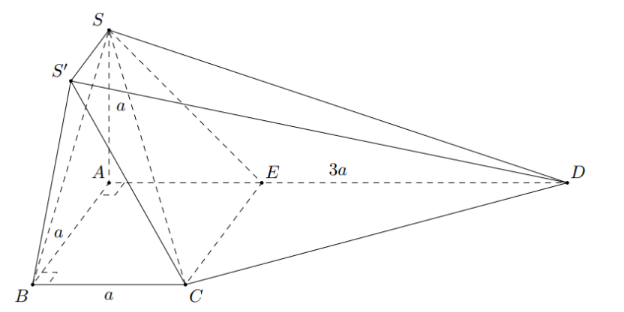
Gọi E là điểm trên cạnh AD sao cho D E=2 A E
Do \(\overrightarrow{S S^{\prime}}=\frac{1}{2} \overrightarrow{A B} \Rightarrow S S^{\prime}=\frac{a}{2}\)
Ta có \(\left\{\begin{array}{l} B C \perp A B \\ B C \perp S A \end{array} \Rightarrow B C \perp\left(S A B S^{\prime}\right)\right.\)
\(V_{S S^{\prime} A B C D}=V_{S . A B C D}+V_{C . B S S^{\prime}}+V_{D . C S S}\)
Trong đó
\(V_{S . A B C D}=\frac{1}{3} S_{A B C D} . S A=\frac{1}{3} \cdot \frac{1}{2} \cdot(B C+A D) \cdot A B \cdot S A=\frac{1}{6} \cdot(a+3 a) \cdot a \cdot a=\frac{2 a^{3}}{3}(\mathrm{đvtt})\)
\(V_{C . B S S}=\frac{1}{3} \cdot S_{B S S^{\prime}} \cdot C B=\frac{1}{3} \cdot \frac{1}{2} \cdot S S^{\prime} \cdot d\left(B, S S^{\prime}\right) \cdot C B=\frac{1}{6} \cdot S S^{\prime} \cdot S A \cdot C B=\frac{1}{6} \cdot \frac{a}{2} \cdot a \cdot a=\frac{a^{3}}{12}(\mathrm{đv} \mathrm{t} \mathrm{t})\)
Do \(d\left(D,\left(C S S^{\prime}\right)\right)=2 d\left(A,\left(C S S^{\prime}\right)\right)\) nên suy ra:
\(V_{D . C S S^{\prime}}=2 V_{A . C S S^{\prime}}=2 V_{C . A S^{\prime}}=2 \cdot \frac{1}{3} \cdot S_{A S^{\prime}} \cdot C B=\frac{2}{3} \cdot \frac{1}{2} \cdot S A \cdot S S^{\prime} \cdot C B=\frac{1}{3} a \cdot \frac{a}{2} \cdot a=\frac{a^{3}}{6}(\mathrm{đv} \mathrm{tt})\)
Vậy \(V_{S S^{\prime} A B C D}=\frac{2 a^{3}}{3}+\frac{a^{3}}{12}+\frac{a^{3}}{6}=\frac{11 a^{3}}{12} \quad(\mathrm{đvtt})\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Nguyễn Trãi