Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm \(SD\) khi đó \(\sin \left( CM,\left( ABCD \right) \right)\) bằng
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai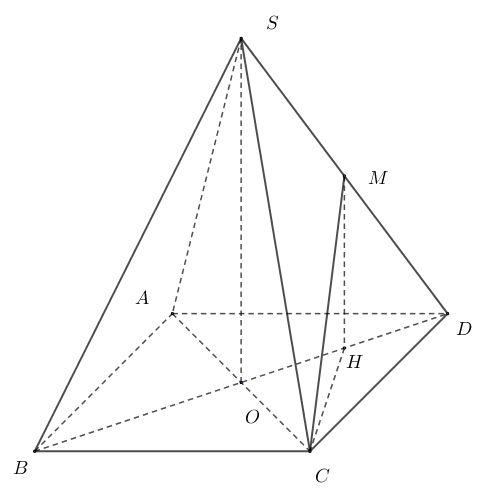
Do \(M\) là trung điểm của \(SD\Rightarrow CM\bot SD\Rightarrow CM=\frac{a\sqrt{3}}{2}\).
Gọi \(H\) là hình chiếu của \(M\) lên mặt phẳng \(\left( ABCD \right)\), suy ra H là trùng với trung điểm \(OD\)
Trong tam giác vuông \(SOD\) có \(SO=\sqrt{S{{D}^{2}}-O{{D}^{2}}}=\sqrt{{{a}^{2}}-{{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}}=\frac{a\sqrt{2}}{2}\Rightarrow MH=\frac{a\sqrt{2}}{4}\).
Ta có \(\sin \left( CM,\left( ABCD \right) \right)=\sin \left( CM,CH \right)=\frac{MH}{CM}=\frac{\frac{a\sqrt{2}}{4}}{\frac{a\sqrt{3}}{2}}=\frac{\sqrt{6}}{6}\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Nguyễn Kiệm
.png)