Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D'\) có các cạnh bằng 2a . Biết \(\widehat{B A D}=60^{\circ}, \widehat{A^{\prime} A B}=\widehat{A^{\prime} A D}=120^{\circ}\) Tính thể tích V của khối hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai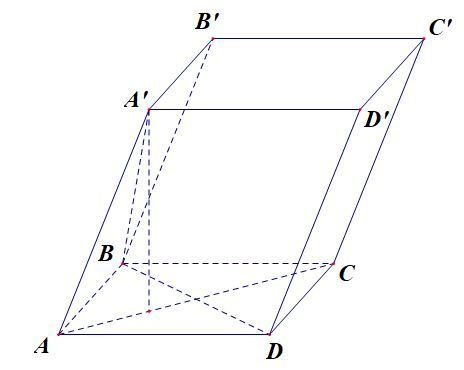
Từ giả thuyết ta có các tam giác \(\Delta A B D, \Delta A^{\prime} A D \text { và } A^{\prime} A B\)là các tam giác đều.
\(\Rightarrow A^{\prime} A=A^{\prime} B=A^{\prime} D\) nên hình chiếu H của A' trên mặt phẳng ( ABCD) là tâm đường tròn ngoại tiếp tam giác đều ABD .
\(\begin{array}{l} \Rightarrow A H=\frac{2}{3} .2 a \cdot \frac{\sqrt{3}}{2}=\frac{2 \sqrt{3}}{3} a \\ \Rightarrow A^{\prime} H=\sqrt{A^{\prime} A^{2}-A H^{2}}=\frac{2 \sqrt{6}}{3} a \end{array}\)
Thể tích khối hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}: \)
\(V=A^{\prime} H S_{A B C D}=\frac{2 \sqrt{6}}{3} a \cdot 2 \cdot \frac{4 a^{2} \cdot \sqrt{3}}{4}=4 \sqrt{2} a^{3}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT chuyên Bến Tre lần 1