Cho hình lăng trụ \({ABC.A'B'C'}\) có \(A{A}'=A{B}'=A{C}'\). Tam giác \({ABC}\) vuông cân tại \({A}\) có \({BC=2a}\). Khoảng cách từ \({A}'\) đến mặt phẳng \(\left( BC{C}'{B}' \right)\) là \(\frac{a\sqrt{3}}{3}\). Tính thể tích khối lăng trụ đã cho.
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai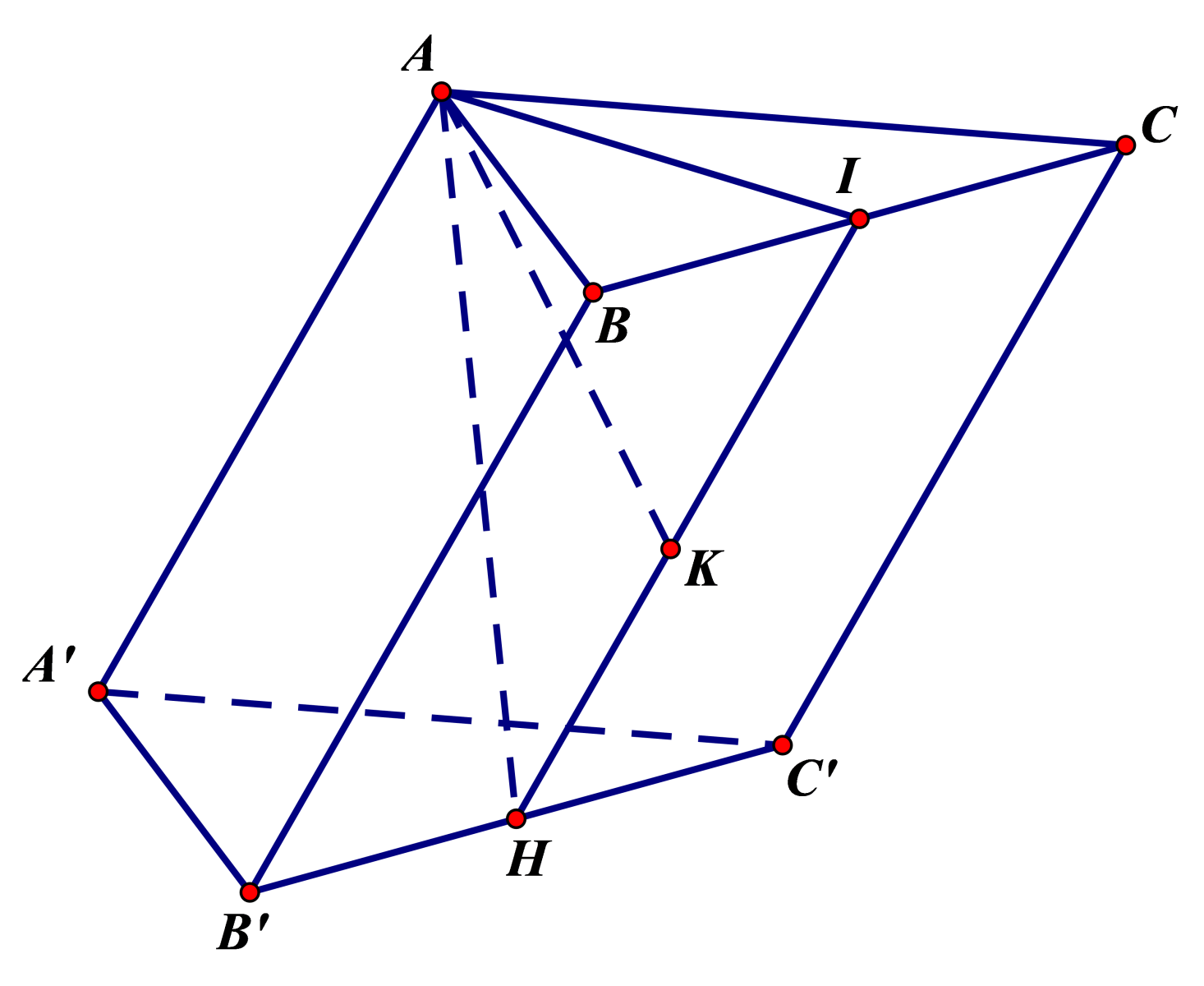
Gọi \(H\)là trung điểm \({B}'{C}'\). Vì tam giác \({A}'{B}'{C}'\)là tam giác vuông cân tại \({A}'\) nên \(H\)là tâm đường tròn ngoại tiếp tam giác \({A}'{B}'{C}'\).
Mặt khác \(A{A}'=A{B}'=A{C}'\), từ đó suy ra \(A,\,\,H\)cách đều 3 điểm \({A}',\,\,{B}',\,\,{C}'\) hay \(AH\bot \left( {A}'{B}'{C}' \right)\).
Gọi \(I\)là trung điểm của \(BC\) khi đó \(AI\bot BC\,\,\left( 1 \right)\)
Mà \({B}'{C}'\bot AH\) và \(BC\)//\({B}'{C}'\) suy ra \(BC\bot AH\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta suy ra \(BC\bot \left( AHI \right)\Rightarrow \left( BC{C}'{B}' \right)\bot \left( AHI \right)\) theo giao tuyến là HI \(\left( 3 \right)\)
Kẻ \(AK\bot HI\), ta được \(AK\bot \left( BC{C}'{B}' \right)\) hay \(d\left( {A}',\,\left( BC{C}'{B}' \right) \right)=d\left( A,\,\left( BC{C}'{B}' \right) \right)=AK=\frac{a\sqrt{3}}{3}\)
Xét tam giác \(AIH\) vuông tại A, ta được \(\frac{1}{A{{H}^{2}}}=\frac{1}{A{{K}^{2}}}-\frac{1}{A{{I}^{2}}}=\frac{3}{{{a}^{2}}}-\frac{1}{{{a}^{2}}}=\frac{2}{{{a}^{2}}}\Rightarrow AH=\frac{a\sqrt{2}}{2}\)
Vậy thể tích khối lăng trụ \(V=\frac{a\sqrt{2}}{2}\cdot \frac{1}{2}.{{\left( a\sqrt{2} \right)}^{2}}=\frac{{{a}^{3}}\sqrt{2}}{2}\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Nguyễn Bỉnh Khiêm