Cho khối chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,\) cạnh bên \(SA=y\,\,\left( y>0 \right).\) và vuông góc với mặt phẳng đáy \(\left( ABCD \right)\). Trên cạnh \(AD\) lấy điểm \(M\) và đặt \(AM=x\,(0 < x < a).\) Tính thể tích lớn nhất \({{V}_{\max }}\) của khối chóp \(S.ABCM,\) biết \({{x}^{2}}+{{y}^{2}}={{a}^{2}}.\)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn A
Theo đề bài, ta có \(0<x<a\)và \(y=\sqrt{{{a}^{2}}-{{x}^{2}}}\).
Khi đó \({{V}_{S.ABCM}}=\frac{1}{3}.{{S}_{ABCM}}.SA=\frac{1}{3}.\frac{\left( x+a \right)a}{2}.y=\frac{1}{6}a\sqrt{{{a}^{2}}-{{x}^{2}}}\left( x+a \right)\)
Ta xét hàm số \(f\left( x \right)=\left( x+a \right)\sqrt{{{a}^{2}}-{{x}^{2}}}\)với \(0<x<a\)
\({f}'\left( x \right)=\frac{-2{{x}^{2}}-ax+{{a}^{2}}}{\sqrt{{{a}^{2}}-{{x}^{2}}}}\)\(\Rightarrow {f}'\left( x \right)=0\Leftrightarrow x=\frac{a}{2}\)
Ta có bảng biến thiên của \(f\left( x \right)\)
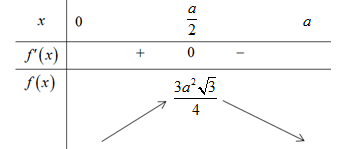
Vậy \(\underset{\left( 0;a \right)}{\mathop{\max }}\,f\left( x \right)=f\left( \frac{a}{2} \right)=\frac{3{{a}^{2}}\sqrt{3}}{4}\) suy ra \(\underset{(0;a)}{\mathop{\max }}\,{{V}_{S.ABCM}}=\frac{{{a}^{3}}\sqrt{3}}{8}\)(đvtt).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Sở GD&ĐT Bắc Ninh lần 1
Câu hỏi liên quan
-
Cho hình chóp \(S.ABC\) có \(AB=4a,BC=3\sqrt{2}a,\)\(\widehat{ABC}=45{}^\circ ;\widehat{SAC}=\widehat{SBC}=90{}^\circ \); Sin góc giữa hai mặt phẳng\(\left( SAB \right)\)và\(\left( SBC \right)\) bằng\(\frac{\sqrt{2}}{4}.\) Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng
-
Cho hình chóp tứ giác \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy và \(SA=3\sqrt{2}a\). Tính thể tích khối chóp \(S.ABCD\).
-
Nghiệm của phương trình \({{\left( \frac{1}{5} \right)}^{{{x}^{2}}-2x-3}}={{5}^{x+1}}\) là
-
Cho hàm số \(y={{x}^{3}}-6{{x}^{2}}+9x+m\text{ }\left( C \right)\), với \(m\) là tham số. Giả sử đồ thị \(\left( C \right)\) cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa mãn \({{x}_{1}}<{{x}_{2}}<{{x}_{3}}\). Khẳng định nào sau đây đúng?
-
Cho biểu thức \(\sqrt[3]{4\sqrt{2\sqrt[5]{8}}}={{2}^{\frac{m}{n}}}\), trong đó \(\frac{m}{n}\) là phân số tối giản. Gọi \(P={{m}^{2}}+{{n}^{2}}\). Khẳng định nào sau đây đúng?
-
Cho khối lăng trụ \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác vuông cân tại \(B\) và \(AC=2a\). Hình chiếu vuông góc của \({A}'\) trên mặt phẳng \(\left( ABC \right)\) là trung điểm \(H\) của cạnh \(AB\) và \(A{A}'=a\sqrt{2}\). Tính thể tích \(V\) của khối lăng trụ đã cho.
-
Gọi \(S\) là tập nghiệm của phương trình \(2{{\log }_{2}}\left( 2x-2 \right)+{{\log }_{2}}{{\left( x-3 \right)}^{2}}=2\) trên \(\mathbb{R}\). Tổng các phần tử của \(S\) bằng
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB=3,\,AD=4\) và các cạnh bên của hình chóp tạo với mặt đáy một góc \(60{}^\circ \). Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.
-
Thể tích \(V\) của khối trụ có chiều cao \(h=4\)cm và bán kính đáy \(r=3\)cm bằng
-
Cho đồ thị hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
Số nghiệm của phương trình \(\left| 2f\left( x \right)-3 \right|=1\) là
-
Gọi \(l,h,r\) lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy. Diện tích xung quanh
\({{S}_{xq}}\) của hình nón là:
-
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ -4;\,4 \right]\) và có bảng biến thiên như hình vẽ bên dưới.
Có tất cả bao nhiêu giá trị thực của tham số \(m\) thuộc đoạn \(\left[ -4;\,4 \right]\) để giá trị lớn nhất của hàm số \(g\left( x \right)=\left| f\left( {{x}^{3}}-3x+2 \right)+2f\left( m \right) \right|\) có giá trị lớn nhất trên đoạn \(\left[ -1;1 \right]\) bằng \(5\)?
-
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(f\left( x \right)=\left( m+1 \right){{x}^{3}}-\left( 2m-1 \right){{x}^{2}}+x-1\) không có điểm cực đại?
-
Cho hình thang ABCD vuông tại A và D có \(CD=2AB=2AD=6.\) Tính thể tích V của khối tròn xoay sinh ra bởi hình thang ABCD khi quanh xung quanh đường thẳng BC
-
Cho hàm số \(y=f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\)và hàm số \(y={f}'\left( x \right)\)là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.
Hàm số \(y=f\left( x \right)\)nghịch biến trên
-
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\left| 3{{x}^{4}}-m{{x}^{3}}+6{{x}^{2}}+m-3 \right|\) đồng biến trên khoảng \(\left( 0;+\infty \right)\)?
-
Lăng trụ tam giác \(ABC.A'B'C'\)có thể tích bằng \(V\). Khi đó, thể tích khối chóp \(A.AB{{C}^{'}}\) bằng:
-
Có bao nhiêu cặp số nguyên \(\left( x;y \right)\) thỏa mãn \(0\le x\le 4000\) và \(5\left( {{25}^{y}}+2y \right)=x+{{\log }_{5}}{{\left( x+1 \right)}^{5}}-4\)?
-
Cho hai mặt phẳng \(\left( P \right)\)và \(\left( Q \right)\) song song với nhau và cùng cắt khối cầu tâm \(O\) bán kính \(4\sqrt{3}\) thành hai hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách \(h\) giữa hai mặt phẳng \(\left( P \right)\)và \(\left( Q \right)\) bằng:
-
Cho cấp số nhân \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=2\) và công bội \(q=-3\). Giá trị của \({{u}_{2}}\) bằng
