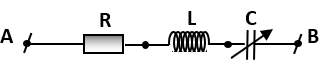
Cho mạch điện AB gồm điện trở thuần R, cuộn thuần cảm L và tụ C nối tiếp với nhau theo thứ tự trên., và có CR² < 2L. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có biểu thức \(u=U\sqrt{2}\cos \left( \omega t \right)\), trong đó U không đổi, w biến thiên. Điều chỉnh giá trị của w để điện áp hiệu dụng giữa hai bản tụ đạt cực đại. Khi đó \({{U}_{C\max }}=\frac{5U}{4}\). Gọi M là điểm nối giữa L và C. Hệ số công suất  của đoạn mạch AM là:

Câu hỏi liên quan

• Sắp xếp theo thứ tự tăng dần về chiết suất của chất làm lăng kính đối với các ánh sáng đỏ (n_đ); tím (n_t); chàm (n_c); lam (n_l)

• Thể tích của hạt nhân \({}_{92}^{238}U\) lớn hơn thể tích của hạt nhân heli \({}_{2}^{4}He\)

• Cho mạch điện như hình vẽ. Mỗi nguồn có \(\xi \)= 24V, r = 2\(\Omega \), R₁ = 2R₄, R₂ = 3\(\Omega \), R₃ = 6\(\Omega \), R_V = \(\infty \), U_V = 4V. Giá trị của R₁ và  R₄ là

  

ZUNIA12

• Điều nào sau đây ℓà đúng khi nói về phương dao động của sóng ngang?

• Tia tử ngoại không có tác dụng nào sau đây?

• Cường độ dòng điện tức thời trong mạch dao động lí tưởng LC là i = 0,08sin(wt)(A). Cuộn dây có độ tự cảm là L=50mH . Điện dung của tụ điện là 5 mF. Hiệu điện thế giữa 2 bản tụ điện ở thời điểm có năng lượng điện trường bằng năng lượng từ trường là

• Chọn phát biểu Sai: Khi mạch RLC xảy ra cộng hưởng thì:

• Một mạch dao động LC có tụ điện \(C=25\ pF\) và cuộn cảm \(L={{4.10}^{-4}}H\). Lúc t=0, dòng điện trong mạch có giá trị cực đại và bằng 20mA. Biểu thức của điện tích trên bản cực của tụ điện là

• Một mạch điện xoay chiều RLC không phân nhánh có R=100\(\Omega \), L=\(\frac{2}{\pi }\)H, tụ điện có điện dung C thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều  \({{u}_{AB}}=200\sqrt{2}\cos (100\pi t+\frac{\pi }{4})\). Giá trị của C và công suất tiêu thụ của mạch khi điện áp giữa hai đầu R cùng pha với điện áp hai đầu đoạn mạch nhận cặp giá trị nào sau đây:

  

• Cho phản ứng hạt nhân: \({}_{92}^{238}U\) → \({}_{82}^{206}Pb\) + 8α + xβ^- . Ban đầu có 2g \({}_{{}}^{238}U\) nguyên chất. Biết chu kì bán rã của urani là T = 4,5.10⁹ năm. Cho số avôgađrô N_A = 6,023.10²³ mol^-1, số hạt β^- phóng ra trong 1 năm là:

• Một nguồn âm điểm S phát sóng âm trong một môi trường đẳng hướng và không hấp thụ âm. Tại điểm M, mức cường độ âm là L_M=30dB. Nếu tăng công suất của nguồn âm lên 2 lần nhưng tần số không đổi thì mức cường độ âm tại M bây giờ gần bằng

• Con lắc đơn được ứng dụng để xác đinh:

• Trong các đơn vị sau, đơn vị của cường độ điện trường là:

• Hai điện trở như nhau được nối song song có điện trở tương đương bằng 2 W. Nếu các điện trở đó mắc nối tiếp thì điện trở tương đương của chúng bằng

• Vật dao động điều hòa có phương trình x=8cos(4\(\pi \)t-\(\frac{2\pi }{3}\)) cm, s. Thời gian ngắn nhất để vật đi được quãng đường bằng biên độ là

• Dây treo con lắc sẽ đứt khi chịu sức căng bằng 2 lần trọng lượng của nó. Biên độ góc \({{\alpha }_{0}}\) để dây đứt khi qua vị trí cân bằng là:

• Lần lượt treo hai vật có khối lượng gấp 3 lần nhau vào lò xo có độ cứng k thì khi cân bằng lò xo có các chiều dài 22,5cm và 27,5cm. Chu kì dao động của con lắc lò xo gồm hai vật cùng treo vào lò xo là  

• Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có điện trở thuần, giữa hai điểm M và N chỉ có cuộn dây, giữa 2 điểm N và B chỉ có tụ điện. Đặt vào hai đầu đoạn mạch một điện áp 175 V – 50 Hz thì điện áp hiệu dụng trên đoạn AM là 25 (V), trên đoạn MN là 25 (V) và trên đoạn NB là 175 (V). Hệ số công suất của toàn mạch là

• Một sóng âm có tần số xác định truyền trong không khí và trong nước với tốc độ lần lượt là 330m/s và 1452m/s. Khi sóng âm đó truyền từ nước ra không khí thì bước sóng của nó sẽ:

• Một sợi dây AB dài ℓ = 2 m, đầu A của sợi dây nối với nguồn rung với tần số f, đầu B tự do. Trên dây hình thành sóng dừng có 3 bụng kể cả đầu B. Nếu tăng chiều dài dây lên 40 cm và giữ đầu B cố định, đồng thời cho đầu A rung với tần số như cũ thì trên dây