Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = - {x^4} + 6{x^2} + mx\) có ba điểm cực trị?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có: \(y' = - 4{x^3} + 12x + m\). Xét phương trình \(y' = 0 \Leftrightarrow - 4{x^3} + 12x + m = 0{\rm{ }}\left( 1 \right)\)
Để hàm số có ba điểm cực trị thì phương trình (1) phải có 3 nghiệm phân biệt.
Ta có: \(\left( 1 \right) \Leftrightarrow m = 4{x^3} - 12x{\rm{ }}\).
Xét hàm số \(g\left( x \right) = 4{x^3} - 12x\)
có \(g'\left( x \right) = 12{x^2} - 12\) .
Cho \(\begin{array}{l}
g'\left( x \right) = 0\\
\Leftrightarrow 12{x^2} - 12 = 0\\
\Leftrightarrow x = \pm 1
\end{array}\)
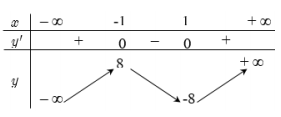
Bảng biến thiên của \(g\left( x \right)\)
Dựa vào bảng biến thiên ta thấy, phương trình (1) có 3 nghiệm phân biệt khi \(-8 < m < 8\).
Do m ∈ \(\mathbb{Z}\) ⇒ m ∈ { - 7, - 6, - 5,...,5,6,7}.
Vậy có 15 giá trị nguyên của tham số m thỏa yêu cầu đề bài.
Đáp án B
Có 15 giá trị nguyên của tham số \(m\)để hàm số \(y = - {x^4} + 6{x^2} + mx\) có ba điểm cực trị.