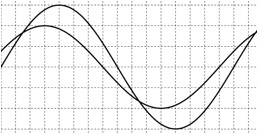
Dao động của một vật có khối lượng 100 g là tổng hợp của hai dao động điều hòa cùng phương có li độ \({{x}_{1}}\) và \({{x}_{2}}\). Hình bên là đồ thị biểu diễn sự phụ thuộc của \({{x}_{1}}\) và \({{x}_{2}}\) theo thời gian \(t\). Theo phương pháp giản đồ Frenel, dao động của vật được biểu diễn bằng một vecto quay. Biết tốc độ góc của vecto quay này là \(\frac{5\pi }{3}\)\(\tfrac{rad}{s}\). Động năng của vật tại thời điểm \(t=0,2\)s là

Câu hỏi liên quan

• Gọi \({{m}_{p}}\) là khối lượng của proton, \({{m}_{n}}\) là khối lượng của nơtron, \({{m}_{X}}\) là khối lượng của hạt nhân  \({}_{Z}^{A}X\)và \(c\) là tốc độ của ánh sáng trong chân không. Đại lượng \(\left( Z{{m}_{p}}+\left( A-Z \right){{m}_{n}}-{{m}_{X}} \right)\frac{{{c}^{2}}}{A}\) được gọi là 

• Trong thí nghiệm Young về giao thoa ánh sáng, khoảng cách giữa hai khe hẹp là \(a\) và cách màn quan sát một khoảng \(D\). Chiếu sáng các khe bằng ánh sáng đơn sắc có bước sóng \(\lambda \). Trên màn, \(M\) và \(N\) là hai vị trí của 2 vân sáng. Biết \(MN=7,7\)mm và khoảng cách giữa 2 vân tối xa nhau nhất trong khoảng \(MN\) là 6,6 mm. Giữ nguyên các điều kiện ban đầu, thay ánh áng có bước sóng \(\lambda \) bằng ánh sáng có bước sóng \({\lambda }'=\frac{4}{5}\lambda \). Vị trí cho vân sáng bậc 5 của bức xạ \({\lambda }'\) cách vân trung tâm

• : Một con lắc đơn có vật nhỏ khối lượng \(m\) đang dao động điều hòa ở nơi có gia tốc trọng trường \(g\). Khi vật qua vị trí có li độ góc \(\alpha \) thì phương trình động lực học cho vật có dạng

  \({\alpha }''+\frac{g}{l}\alpha =0\)

  Đại lượng \(\frac{g}{l}\) có đơn vị là

ZUNIA12

• Đặt điện áp xoay chiều vào hai đầu đoạn mạch có \(RLC\) mắc nối tiếp. Để xác định hệ số công suất của đoạn mạch này, một học sinh dùng dao động kí điện tử để hiển thị đồng thời đồ thị điện áp tức thời giữa hai đầu đoạn mạch và điện áp tức thời giữa hai đầu điện trở \(R\) và cho kết quả như hình bên (các đường hình sin). Hệ số công suất của đoạn mạch này là

  

• Trong điện xoay chiều, các đại lượng nào sau đây không có giá trị hiệu dụng?

• Để xác định thể tích máu trong cơ thể, người ta tiêm vào trong máu một người 10 ml một dung dịch chứa chất phóng xạ \({}^{24}Na\) với nồng độ \({{10}^{-3}}\)\(\tfrac{mol}{l\acute{i}t}\). Cho biết chu kì bán rã của \({}^{24}Na\) là 15 giờ. Sau 6 giờ kể từ thời điểm tiêm vào cơ thể người ta lấy ra 10 ml máu và tìm thấy có \(1,{{78.10}^{-8}}\) mol chất phóng xạ \({}^{24}Na\). Giả thiết với thời gian trên thì chất phóng xạ phân bố đều trong cơ thể. Thể tích máu của người đó là

• Trong điện trường đều, hai điểm \(M\) và \(N\) cùng nằm trên một đường sức điện và đường sức điện có chiều từ \(M\) đến \(N\). Theo chiều từ \(M\) đến \(N\) thì điện thế

• Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm \(A\) và \(B\), dao động cùng pha theo phương thẳng đứng. Trên đoạn \(AB\) quan sát được 13 cực đại giao thoa. Ở mặt nước, đường tròn \((C)\) có tâm \(O\) thuộc trung trực \(AB\) và bán kính \(a\) không đổi (\(2a<AB\)). Khi di chuyển \((C)\) trên mặt nước sao cho tâm \(O\) luôn nằm trên đường trung trực của \(AB\) thì thấy trên \((C)\) có tối đa 12 cực đại giao thoa. Khi trên \((C)\) có 12 điểm cực đại giao thoa thì trong số đó có 4 điểm mà phần tử tại đó dao động ngược pha với nguồn. Đoạn thẳng \(AB\) gần nhất giá trị nào sau đây?

• Trong thí nghiệm Young về giao thoa ánh sáng, nguồn sáng phát ra ánh sáng đơn sắc có bước sóng 500 nm. Hai khe hẹp cách nhau một khoảng \(a\) và cách màn quan sát một khoảng \(D\) với \(D=1200a\). Trên màn, khoảng vân giao thoa là 

• Trong chân không, một tia \(X\) và một tia tử ngoại có bước sóng lần lượt là 0,2 nm và 300 nm. Tỉ số giữa năng lượng mỗi photon của tia \(X\) và năng lượng mỗi photon của tia tử ngoại là 

• Đặt điện áp xoay chiều vào hai đầu đoạn mạch có \(RLC\)mắc nối tiếp thì cảm kháng và dung kháng của đoạn mạch lần lượt là \({{Z}_{L}}\) và \({{Z}_{C}}\). Điện áp giữa hai đầu đoạn mạch trễ pha hơn cường độ dòng điện trong mạch khi 

• Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng. Biết sóng truyền trên mặt nước với bước sóng \(\lambda \). Ở mặt nước, \(M\) là điểm cực đại giao thoa cách hai nguồn những khoảng là \({{d}_{1}}\) và \({{d}_{2}}\). Công thức nào sau đây đúng? 

• Tia lửa điện có bản chất là dòng điện

• Biết cường độ âm chuẩn là \({{10}^{-12}}\)\(\tfrac{W}{{{m}^{2}}}\). Tại một điểm có cường độ âm là \({{10}^{-6}}\)\(\tfrac{W}{{{m}^{2}}}\) thì mức cường độ âm tại đó là 

• Một khung dây dẫn kín hình chữ nhật \(MNPQ\) đặt cố định trong từ trường đều. Hướng của từ trường \(\overrightarrow{{{B}_{{}}}}\) vuông góc với mặt phẳng khung dây như hình bên. Trong khung dây có dòng điện chạy theo chiều \(NMQPN\). Lực từ tác dụng lên cạnh \(MN\) cùng hướng với 

  

• Trong thí nghiệm Young về giao thoa ánh sáng, hai khe hẹp cách nhau một khoảng \(a\) và cách màn quan sát một khoảng \(D\). Chiếu sáng các khe bằng ánh sáng đơn sắc có bước sóng \(\lambda \). Trên màn, khoảng cách từ vị trí có vân tối đến vân trung tâm là 

• Trong y học, tia nào sau đây thường được sử dụng để chiếu điện, chụp điện? 

• Khi nói về ánh sáng đơn sắc, phát biểu nào sau đây sai? 

• Một sợi dây đàn hồi \(AB\) căng ngang có đầu \(B\) cố định, đầu \(A\) nối với một máy rung. Khi máy rung hoạt động, đầu \(A\) dao động điều hòa thì trên dây có sóng dừng với 4 bụng sóng. Đầu \(A\) được coi là một nút sóng. Tăng tần số của máy rung thêm một lượng 12 Hz thì trên dây có sóng dừng với 6 bụng sóng. Biết tốc độ truyền sóng trên dây không đổi. Tần số nhỏ nhất của máy rung để trên dây có sóng dừng là 

• Một con lắc lò xo gồm vật nhỏ và lò xo nhẹ có độ cứng 50 N/m. Khi con lắc dao động điều hòa với biên độ 5 cm thì động năng cực đại của con lắc là