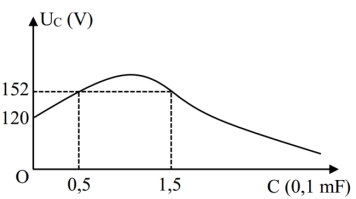
Đặt điện áp xoay chiều có giá trị hiệu dụng bằng 210 V và tần số có thể thay đổi được vào hai đầu mạch điện LRC mắc nối tiếp trong đó điện trở R có thể điều chỉnh. Biết rằng khi tần số có giá trị bằng f hoặc bằng 64f thì đồ thị biểu diễn sự phụ thuộc của hệ số công suất toàn mạch vào điện trở R như mô tả trên hình vẽ. Khi tần số bằng f và điện trở \(R=21\,\Omega \) thì điện áp hiệu dụng trên L bằng
.png)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có hệ số công suất \(cos\varphi =\frac{R}{Z}=\frac{1}{\sqrt{1+\frac{{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{{{R}^{2}}}}}\Rightarrow {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}={{R}^{2}}\left( \frac{1}{co{{s}^{2}}\varphi }-1 \right)\)
Lấy số liệu từ đồ thị thay vào ta có: \({{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}={{63}^{2}}\left( \frac{1}{{{\left( \frac{\sqrt{2}}{2} \right)}^{2}}}-1 \right)={{63}^{2}}\) (1)
Nếu khi tần số là f, cảm kháng và dung kháng của mạch lần lượt là ZL và ZC, thì khi tần số bằng 64f, cảm kháng và dung kháng của mạch lần lượt sẽ là 64ZL và \(\frac{{{Z}_{C}}}{64}\)
Do khi tần số bằng f và 64f thì sự phụ thuộc của hệ số công suất vào R là giống hệt nhau nên ta có:
\({{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}={{\left( 64{{Z}_{L}}-\frac{{{Z}_{C}}}{64} \right)}^{2}}\to {{Z}_{L}}=\frac{{{Z}_{C}}}{64}\) (2)
Từ (1) và (2) ta suy ra \({{Z}_{L}}=1\) và \({{Z}_{C}}=64\)
\({{U}_{L}}=\frac{U}{Z}.{{Z}_{L}}=\frac{U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}{{Z}_{L}}\) \(\to {{U}_{L}}=\frac{210}{\sqrt{{{21}^{2}}+{{63}^{2}}}}.1=\sqrt{10}V\).
Câu hỏi liên quan
-
Nguyên tử hiđrô khi chuyển từ quỹ đạo L có năng lượng là -3,4 eV chuyển về quỹ đạo cơ bản có năng lượng là -13,6 eV thì phát ra một phôtôn ứng với bước sóng bao nhiêu?
-
Trong thí nghiệm Y-âng, nguồn S phát bức xạ đơn sắc là \(\lambda \), màn quan sát cách mặt phẳng hai khe một khoảng không đổi D, khoảng cách giữa hai khe \({{S}_{1}}{{S}_{2}}=a\) có thể thay đổi (nhưng \({{S}_{1}}\) và \({{S}_{2}}\) luôn cách đều S). Xét điểm M trên màn, lúc đầu là vân sáng bậc 4, nếu lần lượt giảm hoặc tăng khoảng cách \({{S}_{1}}{{S}_{2}}\) một lượng \(\Delta a\) thì tại đó là vân sáng bậc k và bậc 3k. Nếu tăng khoảng cách \({{S}_{1}}{{S}_{2}}\) thêm \(2\Delta a\) thì tại M là:
-
Một tàu phá băng công suất 16 MW. Tàu dùng năng lượng phân hạch của hạt nhân \(^{235}U\). Trung bình mỗi phân hạch tỏa ra 200 MeV. Nhiên liệu dùng trong lò là \(^{235}U\) làm giàu đến 12,5% (tính theo khối lượng). Hiệu suất của lò là 30 %. Hỏi nếu tàu làm việc liên tục trong 3 tháng thì cần bao nhiêu kg nhiên liệu (coi mỗi ngày làm việc 24 giờ, 1 tháng tính 30 ngày)
-
Để cho chu kì bán rã T của một chất phóng xạ, người ta dùng máy đếm xung. Trong t1 giờ đầu tiên máy đếm được n1 xung; trong t2 = 2t1 giờ tiếp theo máy đếm được n2 = \(\frac{9}{64}\)n1 xung. Chu kì bán rã T có giá trị là bao nhiêu?
-
Dùng hạt proton có động năng 1,6MeV bắn vào hạt nhân liti \({}_{3}^{7}Li\) đứng yên. Giả sử sau phản ứng thu được hai hạt nhân giống nhau có cùng động năng và không kèm theo tia γ . Biết năng lượng tỏa ra của phản ứng là 17,4MeV. Động năng của mỗi hạt sinh ra là
-
Quang phổ gồm một dãi màu từ đỏ đến tím là
-
Điện năng được truyền từ nơi phát đến một khu dân cư bằng đường dây một pha với hiệu suất truyền tải là η. Coi hao phí điện năng chỉ do tỏa nhiệt trên đường dây. Nếu công suất truyền tải giảm n lần so với ban đầu và giữ nguyên điện áp ở nơi phát thì hiệu suất truyền tải điện năng trên chính đường dây đó là
-
Hai chất điểm dao động điều hòa cùng tần số có li độ phụ thuộc thời gian được biểu diễn trên hình vẽ. Khi chất điểm thứ nhất có tốc độ bằng \(\frac{4\pi }{9}cm/s\) và đang tăng thì tốc độ của chất điểm thứ hai xấp xỉ bằng bao nhiêu?
.png)
-
Từ trường là dạng vật chất tồn tại trong không gian và
-
Trong thí nghiệm Iâng về giao thoa ánh sáng khoảng cách giữa hai khe là 1mm, khoảng cách từ hai khe đến màn là 2m. Nếu chiếu đồng thời hai bức xạ đơn sắc có bước sóng l1 = 0,6mm và l2 = 0,5mm thì trên màn có những vị trí tại đó có vân sáng của hai bức xạ trùng nhau gọi là vân trùng. Tìm khoảng cách nhỏ nhất giữa hai vân trùng.
-
Trong thí nghiệm giao thoa Iâng, thực hiện đồng thời với hai bức xạ đơn sắc trên màn thu được hai hệ vân giao thoa với khoảng vân lần lượt là 1,35 (mm) và 2,25 (mm). Tại hai điểm gần nhau nhất trên màn là M và N thì các vân tối của hai bức xạ trùng nhau. Tính MN:
-
Chiếu một chùm bức xạ đơn sắc có bước sóng 0,5µm vào kim loại có bước sóng 0,66µm, lấy c = 3.108 m/s, h = 6,625.10-34 Js. Công thoát của electron quang điện là:
-
Số chỉ của ampe kế và vôn kế sẽ thay đổi như thế nào ( Am pe kế mắc nối tiếp; vôn kế mắc song song với nguồn) nếu tắt chùm sáng kích thích AS?
-
Một con lắc lò xo gồm vật nhỏ khối lượng m và lò xo có độ cứng k. Con lắc dao động điều hòa với chu kì là
-
Phát biểu nào sau đây là sai khi nói về sóng cơ ?
-
Tại một điểm có 2 cường độ điện trường thành phần vuông góc với nhau và có độ lớn là 3000 V/m và 4000V/m. Độ lớn cường độ điện trường tổng hợp là
-
Hạt nhân đơteri \({}_{1}^{2}D\) có khối lượng mD = 2,0136u, khối lượng của nơtron là mN = 1,0087u, khối lượng của proton là mP = 1,0073u. Tính năng lượng liên kết của hạt nhân \({}_{1}^{2}D\).Biết 1u= 931,5 MeV/c2.
-
Trong thí nghiệm Young về giao thoa ánh sáng, khoảng cách giữa hai khe là a = 2 mm, khoảng cách từ hai khe đến màn quan sát là D = 1,5 m. Nguồn sáng đơn sắc có bước sóng l = 0,6 mm. Xét trên khoảng MN trên màn, với MO = 5 mm, ON = 10 mm, (O là vị trí vân sáng trung tâm giữa M và N). Hỏi trên MN có bao nhiêu vân sáng, bao nhiêu vân tối?
-
Dòng điện cảm ứng trong mạch kín có chiều
-
Đặt hiệu điện thế u = U0cos(100t) V, t tính bằng s vào hai đầu đoạn R, L, C mắc nối tiếp, cuộn dây thuần cảm. Trong đó U0, R, L không đổi, C có thể thay đổi được. Cho sơ đồ phụ thuộc của UC vào C như hình vẽ (chú ý, 48\(\sqrt{10}\) = 152). Giá trị của ZC là
