Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi tần số f = 50Hz vào hai đầu đoạn mạch nối tiếp gồm biến trở R, cuộn dây không thuần cảm có r = 30Ω độ tự cảm \(L=\frac{1,2}{\pi }H.\) Tụ có điện dung \(C=\frac{{{10}^{-4}}}{\pi }F.\) Gọi P là tổng công suất trên biến trở và trên mạch. Hình bên là một phần đồ thị P theo R. Khi biến trở có giá trị R1 thì tổng hệ số công suất trên cuộn dây và trên mạch gần nhất giá trị nào sau đây?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có: \(\left\{ \begin{array}{*{35}{l}} r=30\Omega \\ {{Z}_{L}}=120\Omega \\ {{Z}_{C}}=100\Omega \\ \end{array} \right.\)
Công suất trên biến trở: \({{P}_{R}}={{I}^{2}}R=\frac{{{U}^{2}}}{{{(R+r)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}R\)
Công suất trên mạch: \({P}'={{I}^{2}}(R+r)=\frac{{{U}^{2}}}{{{(R+r)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}(R+r)\)
Ta có: \(P={{P}_{R}}+{P}'=\frac{{{U}^{2}}}{{{(R+r)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}(2R+r)\) \(\Rightarrow P=\frac{{{U}^{2}}}{{{(R+30)}^{2}}+{{20}^{2}}}(2R+30)\)
\(\Rightarrow P=\frac{{{U}^{2}}}{{{R}^{2}}+60R+1300}2(R+15)\)
\(\Rightarrow P=\frac{{{U}^{2}}}{\left( {{R}^{2}}+30R+{{15}^{2}} \right)+30(R+15)+625}2(R+15)\)
\(\Rightarrow P=\frac{2{{U}^{2}}}{(R+15)+\frac{625}{R+15}+30}\)
Ta có: \({{P}_{\max }}~khi~{{\left( (R+15)+\frac{625}{(R+15)} \right)}_{\min }}\)
Lại có: \((R+15)+\frac{625}{R+15}\ge 2\sqrt{(R+15)\frac{625}{(R+15)}}=50\)
Dấu = xảy ra khi \((R+15)=\frac{625}{R+15}\Rightarrow R=10\Omega \)
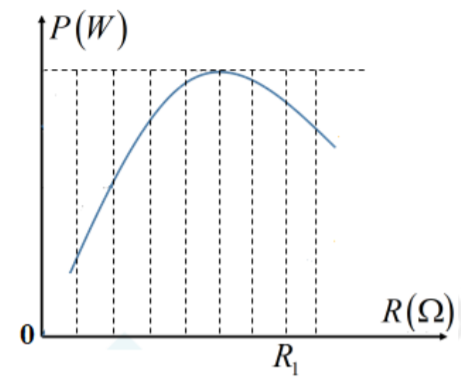
Từ đồ thị ta có: \(\frac{{{R}_{1}}}{R}=\frac{7}{5}\Rightarrow {{R}_{1}}=\frac{7}{5}R=\frac{7}{5}.10=14\Omega \)
Khi \(R={{R}_{1}}=14\Omega :\)
+ Tổng trở: \(Z=\sqrt{{{\left( {{R}_{1}}+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\sqrt{{{(14+30)}^{2}}+{{20}^{2}}}=4\sqrt{146}\Omega \)
+ Hệ số công suất trên cuộn dây: \(\cos {{\varphi }_{d}}=\frac{r}{Z}=\frac{30}{4\sqrt{146}}\)
+ Hệ số công suát trên mạch: \(\cos \varphi =\frac{{{R}_{1}}+r}{Z}=\frac{14+30}{4\sqrt{146}}\)
Tổng hệ số công suất trên cuộn dây và trên mạch: \(\frac{30}{4\sqrt{146}}+\frac{44}{4\sqrt{146}}=1,531\)
Đề thi thử THPT QG năm 2021 môn Vật Lý
Trường THPT Chuyên Lam Sơn Lần 2
Câu hỏi liên quan
-
Một kính hiển vi gồm vật kính có tiêu cự \({{f}_{1}}=0,5cm\) và thị kính có tiêu cự \({{f}_{2}}=2cm,\)khoảng cách giữa vật kính và thị kính là 12,5cm. Độ bội giác của kính khi ngắm chừng ở vô cực là
-
Mạch dao động gồm cuộn cảm có độ tự cảm L và tụ điện có điện dung C. Tần số góc dao động riêng của mạch xác định bởi
-
Đặt điện áp xoay chiều có điện áp hiệu dụng \(U=120V\) vào hai đầu đoạn mạch RLC nối tiếp thì cường độ dòng điện hiệu dụng qua mạch đo được là 1,2A. Biết điện áp hai đàu đoạn mạch nhanh pha \(\frac{2\pi }{3}rad\)so với điện áp hai đầu mạch RC, điện áp hiệu dụng \({{U}_{RC}}=120V.\) Giá trị điện trở thuần là
-
Một khung dây dẫn phẳng diện tích 20cm2 gồm 100 vòng đặt trong từ trường đều có cảm ứng từ \(B={{2.10}^{-4}}T.\) Véctơ cảm ứng từ hợp với pháp tuyến khung dây một góc \({{60}^{0}}.\) Người ta giảm đều cảm ứng từ đến 0 trong khoảng thời gian 0,01 giây. Suất điện động cảm ứng xuất hiện trong khung trong thời gian từ trường biến đổi là
-
Đặt điện áp xoay chiều \(u={{U}_{0}}\cos 2\pi ft(V)\) có U0 không đổi và f thay đổi được vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Khi \(f={{f}_{0}}\) thì trong đoạn mạch có cộng hưởng điện. Giá trị của \({{f}_{0}}\)là
-
Một máy biến áp lí tưởng có số vòng dây của cuộn sơ cấp và cuộn thứ cấp lần lượt là N1 và N2. Nếu máy biến áp này là máy hạ áp thì:
-
Khi một sóng cơ truyền từ không khí vào nước thì đại lượng nào sau đây không đổi?
-
Sóng cơ truyền được trong các môi trường
-
Biết \({{I}_{0}}\)là cường độ âm chuẩn. Tại điểm có cường độ âm I thì mức cường độ âm là
-
Hai bóng đèn có các hiệu điện thế định mức lần lượt là U1 và U2. Nếu công suất định mức của hai bóng đó bằng nhau thì tỷ số hai điện trở \(\frac{{{R}_{1}}}{{{R}_{2}}}\) là
-
Chiếu bức xạ có tần số f vào một kim loại có công thoát A gây ra hiện tượng quang điện. Giả sử một electron hấp thụ photôn sử dụng một phần năng lượng làm công thoát, phần còn lại biến thành động năng K của nó. Nếu tần số của bức xạ chiếu tới là 2f thì động năng của electron quang điện đó:
-
Một tụ điện có dung kháng 200Ω mắc nối tiếp với một cuộn dây. Đặt vào hai đầu mạch điện này hiệu điện thế \(u=120\sqrt{2}\cos (100\pi t)V\) thì cường độ dòng điện qua mạch là \(i=0,6\cos \left( 100\pi t-\frac{\pi }{6} \right)A.\) Hiệu điện thế hiệu dụng ở hai đầu cuộn dây có giá trị gần nhất giá trị nào sau đây?
-
Một con lắc lò xo gồm vật nhỏ có khối lượng m và lò xo nhẹ có độ cứng k. Chu kì dao động riêng của con lắc là
-
Hai dao động điều hòa cùng phương, cùng tần số có biên độ \({{A}_{1}}=8cm;{{A}_{2}}=15cm.\) Dao động tổng hợp của hai dao động này có biên độ không thể nhận giá trị nào sau đây?
-
Một sóng điện từ có tần số 75k Hz đang lan truyền trong chân không. Lấy \(c={{3.10}^{8}}\text{m/s}\text{.}\)Sóng này có bước sóng là
-
Một sợi dây dài l có 2 đầu cố định. Trên dây đang có sóng dừng với 4 bụng sóng. Sóng truyền trên dây có bước sóng là 20cm. Giá trị của l là
-
Trên mặt nước có hai nguồn sóng A, B cách nhau 20cm dao động theo phương thẳng đứng v ới phương trình \(u=1,5\cos \left( 20\pi t+\frac{\pi }{6} \right)cm.\) Sóng truyền đi với vận tốc 20 cm/s. Gọi O là trung điểm AB, M là một điểm nằm trên đường trung trực AB (khác O) sao cho M dao động cùng pha với hai nguồn và gần nguồn nhất; N là một điểm nằm trên AB dao động với biên độ cực đại gần O nhất. Coi biên độ sóng không thay đổi trong quá trình truyền đi. Khoảng cách giữa 2 điểm M, N lớn nhất trong quá trình dao động gần nhất với giá trị nào sau đây?
-
Một lò xo nhẹ, có độ cứng k =100N/m được treo vào một điểm cố định, đầu dưới treo vật nhỏ khối lượng m = 400g. Giữ vật ở vị trí lò xo không biến dạng rồi buông nhẹ để vật dao động điều hòa tự do dọc theo trục lò xo. Chọn trục tọa độ thẳng đứng chiều dương hướng xuống, gốc thời gian là lúc buông vật. Tại thời điểm t = 0,2s, một lực \(\overrightarrow{F}\) thẳng đứng, có cường độ biến thiên theo thời gian biểu diễn như đồ thị trên hình bên, tác dụng vào vật. Biết điểm treo chỉ chịu được lực kéo tối đa có độ lớn 20N (lấy \(g={{\pi }^{2}}=10\text{m/}{{\text{s}}^{\text{2}}}\)). Tại thời điểm lò xo bắt đầu rời khỏi điểm treo, tổng quãng đường vật đi được kể từ t = 0 là
.png)
-
Hình bên là đồ thị biểu diễn sự phụ thuộc của vận tốc v theo thời gian t của một vật dao động điều hòa. Phương trình dao động của vật là
.png)
-
Điện năng được truyền từ nơi phát đến một khu dân cư bằng đường dây một pha với hiệu suất truyền tải là 95%. Coi hao phí điện năng chỉ do tỏa nhiệt trên đường dây và không vượt quá 30%. Nếu công suất sử dụng điện của khu dân cư này tăng thêm 20% và giữ nguyên điện áp ở nơi phát thì hiệu suất truyền tải điện năng trên chính đường dây khi đó gần nhất giá trị nào sau đây?
