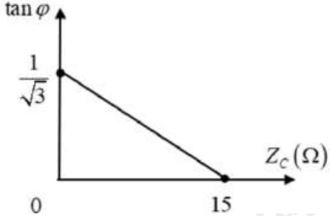
Đặt một điện áp xoay chiều ổn định \(u=U\sqrt{2}\cos (\omega t)\) V vào hai đầu một đoạn mạch ghép nối tiếp gồm điện trở R, một cuộn cảm thuần có độ tự cảm L và một tụ điện có điện dung C thay đổi được. Gọi i là cường độ dòng điện tức thời qua mạch, \(\varphi \) là độ lệch pha giữa u và i. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của tan\(\varphi \) theo Z_C. Thay đổi C để điện áp hai đầu đoạn mạch vuông pha với điện áp hai đầu đoạn mạch RL, giá trị của dung kháng khi đó là 

Câu hỏi liên quan

• Đặt vào hai đầu đoạn mạch R, L, C không phân nhánh một điện áp xoay chiều, biết cảm kháng của cuộn cảm thuần là Z_L, dung kháng của tụ điện là Z_C và điện trở thuần R. Biết i trễ pha so với với u. Mỗi quan hệ đúng là

• Dao động của con lắc đồng hồ là dao động 

• Một vật khối lượng 100g dao động điều hòa theo phương trình x = 3cos(2πt) (trong đó x tính bằng cm và t tính bằng s). Lấy π² =10. Mốc thế năng ở vị trí cân bằng. Cơ năng của vật là

ZUNIA12

• Đặt điện áp \({{u}_{AB}}=40\sqrt{2}\cos (100\pi t)V\) vào hai đầu đoạn mạch AB không phân nhánh gồm điện trở thuần, tụ điện và cuộn dây thuần cảm có độ tự cảm L thay đổi được. M ở giữa tụ điện và cuộn cảm thuần. Khi L = L₀ thì tổng trở của đoạn mạch AB đạt giá trị cực tiểu và điện áp hiệu dụng giữa hai đầu đoạn mạch AM là 80V. Khi L = 2L₀  thì điện áp cực đại hai đầu đoạn mạch MB là

• Trong thí nghiệm khảo sát chu kì dao động T của con lắc đơn, một học sinh làm thí nghiệm và vẽ đồ thị phụ thuộc của T² (trục tung) theo chiều dài 1 (trục hoành) của con lắc, thu được một đường thẳng kéo dài đi qua gốc tọa độ, hợp với trục tung một góc \(\beta ={{14}^{0}},\) lấy π = 3,14. Gia tốc trọng trường tại nơi làm thí nghiệm xấp xỉ là

• Một sóng ngang truyền trên sợi dây với tốc độ và biên độ không đổi, bước sóng 72cm. Hai phần tử sóng M, N gần nhau nhất lệch pha nhau \(\frac{\pi }{3}.\) Tại một thời điểm li độ của M, N đối nhau và cách nhau 13,0cm. Biên độ sóng là

• Một chất điểm dao động điều hòa có đồ thị li độ theo thời gian như hình vẽ. Tốc độ của vật tại N là 

  

• Trong một thí nghiệm giao thoa với hai nguồn đồng bộ phát sóng kết hợp có bước sóng 2cm. Trong vùng giao thoa, M là điểm cách S₁ và S₂ lần lượt là 5cm và 17cm. Giữa M và đường trung trực của đoạn \({{S}_{1}}{{S}_{2}}\) có số vấn giao thoa cực tiểu là

• Sóng cơ truyền trên một sợi dây rất dài với khoảng cách giữa hai đỉnh sóng liên tiếp là 20cm. Bước sóng \(\lambda \) bằng

• Một chất điểm thực hiện đồng thời hai dao động điều hòa có phương trình \({{x}_{1}}={{A}_{1}}\cos \left( 6t-\frac{\pi }{2} \right)cm\) và \({{x}_{2}}=2\sqrt{3}\cos (6t)cm.\) Chọn mốc thế năng ở vị trí cân bằng, khi động năng của con lắc bằng một phần ba cơ năng, thì vật có tốc độ \(12\sqrt{3}\)cm/s. Biên độ dao động A₁ bằng 

• Dùng vôn kế xoay chiều đo điện áp giữa hai đầu của đoạn mạch xoay chiều và chỉ 50V. Giá trị đo được là giá trị

• Đơn vị của hiệu điện thế là

• Một con lắc đơn chiều dài l đang dao động điều hòa tại nơi gia tốc rơi tự do g. Một con lắc lò xo có độ cứng k và vật có khối lượng m đang dao động điều hòa. Biểu thức \(\sqrt{\frac{k}{m}}\) có cùng đơn vị với biểu thức 

• Khi ghép n nguồn điện giống nhau song song, mỗi nguồn có suất điện động \(\xi \) và điện trở trong r thì suất điện động và điện trở trong của bộ nguồn là 

• Trong không khí khi hai điện tích điểm đặt cách nhau lần lượt là d và d +10cm thì lực tương tác giữa chúng có độ lớn tương ứng là 4.10^-6N và 10^-6N. Giá trị của d là

• Âm sắc của âm là một đặc trưng sinh lý của âm phụ thuộc vào

• Cho mạch điện xoay chiều RLC mắc nối tiếp với cuộn cảm thuần, cho R = 50Ω. Đặt vào hai đầu đoạn mạch điện áp \(u=100\sqrt{2}\cos \omega \text{t}\) (V), biết điện áp giữa hai đầu cuộn dây và điện áp giữa hai đầu đoạn mạch lệch pha nhau một góc \(\frac{\pi }{3}.\) Công suất tiêu thụ của mạch điện là 

• Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R và tụ điện mắc nối tiếp thì dung kháng của tụ điện là Z_C. Hệ số công suất của đoạn là 

• Một máy biến áp lí tưởng có số vòng dây của cuộn sơ cấp có tổng số vòng dây của hai cuộn là 2400 vòng. Nếu đặt vào hai đầu cuộn sơ cấp một điện áp xoay chiều có giá trị hiệu dụng 240V thì điện áp hiệu dụng ở hai đầu cuộn thứ cấp để hở là 80V. Số vòng dây cuộn sơ cấp là

• Một khung dây dẫn phẳng, diện tích 50cm², gồm 500 vòng dây, quay đều với tốc độ 50 vòng/giây quanh một trục cố định \(\Delta \) trong từ trường đều có cảm ứng từ \(\vec{B}.\) Biết \(\Delta \) nằm trong mặt phẳng khung dây và vuông góc với \(\vec{B}.\) Suất điện động cực đại trong khung là \(200\sqrt{2}V.\) Độ lớn của \(\overrightarrow{B}\)