Điện năng được truyền từ trạm phát điện đến nơi tiêu thụ bằng đường dây tải điện một pha. Ban đầu hiệu suất truyền tải là 60%. Cho công suất truyền đi không đổi và hệ số công suất ở nơi tiêu thụ (cuối đường dây tải điện) luôn bằng 0,8. Để giảm hao phí trên đường dây 4 lần thì cần phải tăng điện áp hiệu dụng ở trạm phát điện lên n lần. Giá trị của n là
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa biễu diễn mối liên hệ giữa các điện áp trong quá trình truyền tải
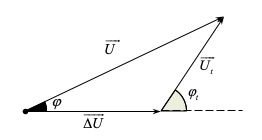
\(U\sin \varphi = {U_t}\sin {\varphi _t}\)
Ptt = HP→\({U_t}I\cos {\varphi _t} = H\left( {UI\cos \varphi } \right)\) → \(U\cos \varphi = \frac{{{U_t}\cos {\varphi _t}}}{H}\)
→ từ hai phương trình trên, ta có \(\tan \varphi = H\tan {\varphi _t}\).
Tiến hành lập bảng tỉ lệ
.png)
Ta có: \({\left( {\frac{{\cos {\varphi _2}}}{{\cos {\varphi _1}}}} \right)^2} = \frac{4}{{{n^2}}} = \frac{{1 + {{\tan }^2}{\varphi _1}}}{{1 + {{\tan }^2}{\varphi _2}}} = \frac{{1 + 0,{{48}^2}}}{{1 + 0,{{72}^2}}}\)=> n ≈ 2,2
Đề thi thử tốt nghiệp THPT QG môn Vật Lý năm 2020
Tuyển chọn số 2