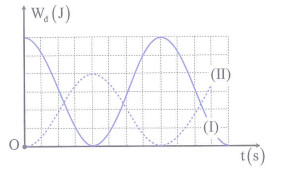
Hai con lắc lò xo dao động điều hòa có động năng biến thiên theo thời gian như đồ thị, con lắc (I) là đường liền nét và con lắc (II) là đường nét đứt. Vào thời điểm thế năng của hai con lắc bằng nhau thì tỉ số động năng của con lắc (II) và động năng của con lắc (I) là
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTừ đồ thị ta thấy rằng tại t = 0, động năng của vật I cực đại (vật I đang ở VTCB), động năng của vật II cực tiểu và bằng 0 (vật II đang ở vị trí biên) nên dao động của con lắc I và II vuông pha nhau.
Gọi \({{\text{W}}_{1}}\) và \({{\text{W}}_{2}}\) lần lượt là cơ năng của con lắc I và con lắc II, ta có: \({{\text{W}}_{1}}=6\) ô, \({{\text{W}}_{2}}=4\) ô
\(\Rightarrow \frac{{{\text{W}}_{1}}}{{{\text{W}}_{2}}}=\frac{6}{4}=1,5\)
+ Ta biểu diễn động năng và thế năng của các vật theo cơ năng:
\(\left\{ \begin{array}{l} {{\rm{W}}_t} = W{\cos ^2}\varphi \\ {W_{}} = W{\sin ^2}\varphi \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {W_{{t_1}}} = {W_{{t_2}}}\\ \frac{{{W_{_2}}}}{{{W_{_1}}}} = \frac{{{W_2}{{\sin }^2}{\varphi _2}}}{{{W_1}{{\sin }^2}{\varphi _1}}} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {W_1}{\cos ^2}{\varphi _1} = {W_2}{\cos ^2}{\varphi _2}(1)\\ \frac{{{W_{_2}}}}{{{W_{_1}}}} = \frac{{{W_2}(1 - {{\cos }^2}{\varphi _2})}}{{{W_1}(1 - {{\cos }^2}{\varphi _1})}}(2) \end{array} \right.\)
Hai dao động vuông pha nên ta có: \({{\cos }^{2}}{{\varphi }_{1}}+{{\cos }^{2}}{{\varphi }_{2}}=1\)
Từ (1) ta có:
\({{W}_{1}}{{\cos }^{2}}{{\varphi }_{1}}={{W}_{2}}{{\cos }^{2}}{{\varphi }_{2}}\Leftrightarrow 1,5{{W}_{2}}.{{\cos }^{2}}{{\varphi }_{1}}={{W}_{2}}(1-{{\cos }^{2}}{{\varphi }_{1}})\Leftrightarrow 2,5.{{\cos }^{2}}{{\varphi }_{1}}=1\Rightarrow {{\cos }^{2}}{{\varphi }_{1}}=0,\)
\(\Rightarrow {{\cos }^{2}}{{\varphi }_{2}}=1-{{\cos }^{2}}{{\varphi }_{1}}=1-0,4=0,6\)
Từ (2) \(\Rightarrow \frac{{{W}_{{{\text{}}_{2}}}}}{{{W}_{{{\text{}}_{1}}}}}=\frac{{{W}_{2}}(1-0,6)}{1,5.{{W}_{2}}(1-0,4)}=\frac{4}{9}\)
Đề thi thử THPT QG năm 2022 môn Vật Lý
Trường THPT Lê Trung Đình