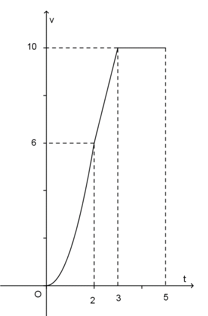
Một chiếc xe đua \({{F}_{1}}\) đạt tới vận tốc lớn nhất là \(360\,km/h\). Đồ thị bên biểu thị vận tốc \(v\) của xe trong \(5\) giây đầu tiên kể từ lúc xuất phát. Đồ thị trong \(2\) giây đầu tiên là một phần của parabol đỉnh tại gốc tọa độ \(O\), giây tiếp theo là đoạn thẳng và sau đúng \(3\) giây thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị \(1\) giây, mỗi đơn vị trục tung biểu thị \(10\,m/s\) và trong \(5\) giây đầu xe chuyển động theo đường thẳng. Hỏi trong \(5\) giây đó xe đã đi được quãng đường là bao nhiêu?

Câu hỏi liên quan

• Đồ thị hàm số \(y=\frac{x+3}{{{x}^{3}}-3x}\) có bao nhiêu đường tiêm cận?

• Cho hàm số \(f\left( x \right)\) nhận giá trị dương và có đạo hàm liên tục trên \(\left[ 1;\ e \right]\). Biết \(f\left( 1 \right)=1\) và \(x.f\left( x \right).{f}'\left( x \right)={{x}^{2}}+{{f}^{2}}\left( x \right)\) với mọi \(x\in \left[ 1;\ e \right].\) Khi đó, \(\int\limits_{1}^{e}{\frac{f\left( x \right)}{{{x}^{2}}}dx}\) bằng

• Có bao nhiêu số phức \(z\)đôi một khác nhau thỏa mãn \(\left| z+i \right|=2\) và \({{\left( z-2 \right)}^{4}}\) là số thực?

ZUNIA12

• Có bao nhiêu số nguyên \(m\)để hàm số \(f\left( x \right)=3x+m\sqrt{{{x}^{2}}+1}\) đồng biến trên \(\mathbb{R}\)?

• Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):ax+by+cz+7=0\) qua điểm \(A\left( 2;0;1 \right)\), vuông góc với mặt phẳng \(\left( Q \right):3x-y+z+1=0\) và tạo với mặt phẳng \(\left( R \right):x-y+2z-1=0\) một góc \({{60}^{\text{o}}}\). Tổng \(a+b+c\) bằng

• Chu vi đường tròn lớn của mặt cầu \(S\left( O;R \right)\) là

• Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình bên. Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ -3;3 \right]\) bằng

  

• Gọi \({{z}_{1}}\), \({{z}_{2}}\) là các nghiệm phức của phương trình \({{z}^{2}}-3z+5=0\). Môđun của số phức \(\left( 2{{{\bar{z}}}_{1}}-3 \right)\left( 2{{{\bar{z}}}_{2}}-3 \right)\) bằng

• Một khối trụ có đường cao bằng \(2\), chu vi của thiết diện qua trục gấp \(3\)lần đường kính đáy. Thể tích của khối trụ đó bằng

• Một tổ học sinh có 12 bạn, gồm 7 nam và 5 nữ. Cần chọn một nhóm 3 học sinh của tổ đó để làm vệ sinh lớp học. Hỏi có bao nhiêu cách chọn sao cho trong nhóm có cả nam và nữ?

• Cho góc ở đỉnh của một hình nón bằng \({{60}^{0}}\). Gọi \(r,h,l\) lần lượt là bán kính đáy, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?

• Xét các số phức \(z=a+bi,\,\,\left( a,\,\,b\in \mathbb{R} \right)\) thỏa mãn \(\left| z-2+3i \right|=4\) và \(\left| z+1-4i \right|+\left| z-9 \right|\) đạt giá trị lớn nhất. Khi đó \(5a-2b\) bằng

• Cho hàm số \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) (với \(a,b,c,d\in \mathbb{R}\)) có đồ thị như hình vẽ

  

  Có bao nhiêu số dương trong các số \(a,b,c,d\)?

• Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có \(AB=A{A}'=2a\), \(AC=a\), \(\widehat{BAC}=120{}^\circ \). Bán kính mặt cầu ngoại tiếp hình chóp \(A.BC{C}'{B}'\) bằng

• Họ các nguyên hàm của hàm số \(f\left( x \right)={{3}^{2x-1}}\) là

• Xét tất cả các số thực dương \(x;y\) thỏa mãn \(\frac{x+y}{10}+\log \left( \frac{1}{2x}+\frac{1}{2y} \right)=1+2xy\). Khi biểu thức \(\frac{4}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}\) đạt giá trị nhỏ nhất, tích \(xy\) bằng

• Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\). Góc giữa hai đường thẳng \(AB\) và \({B}'{D}'\) bằng

• Hàm số \(f\left( x \right)={{x}^{4}}{{\left( x-1 \right)}^{2}}\) có bao nhiêu điểm cực trị?

• Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình bên. Hỏi phương trình \(2f\left( x \right)=5\) có bao nhiêu nghiệm trên đoạn \(\left[ -1;2 \right]\)?

  

• Trong không gian \(Oxyz\), một véctơ pháp tuyến của mặt phẳng \(\left( Oyz \right)\) là