Một con lắc đơn có chiều dài sợi dây 50 cm và khối lượng vật nặng M được treo vào điểm I. Một vật nặng có khối lượng m nối với vật M bằng một sợi dậy và vắt qua ròng rọc tại điểm K. Ban đầu hệ cân bằng và các vật đứng yên, sau đó đốt sợi dây giữa m và M để vật M dao động điều hòa. Cho \(m=0,23M,IK=50~\text{cm v }\!\!\grave{\mathrm{a}}\!\!\text{ }IK\) nằm ngang. Bỏ qua ma sát, lực cản, khối lượng dây. Lấy \(g=9,8~\text{m}/{{\text{s}}^{2}}.\)Tốc độ dao động của điểm M khi qua vị trí dây treo thẳng đứng bằng
.png)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai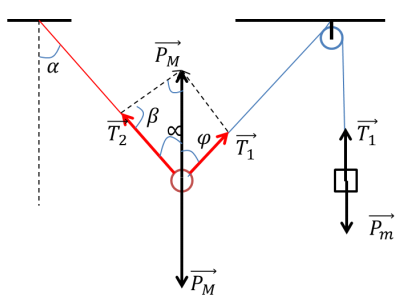
Từ hình vẽ ta có: \(\beta ={{135}^{0}}-\frac{\alpha }{2}\)
Áp dụng định lý hàm số sin ta có:
\(\frac{{{T}_{1}}}{\sin \alpha }=\frac{{{P}_{M}}}{\sin \beta }\leftrightarrow \frac{{{P}_{m}}}{\sin \alpha }=\frac{{{P}_{M}}}{\sin \left( {{135}^{0}}-\frac{\alpha }{2} \right)}\to \alpha =10,{{16}^{0}}\)
Khi ta đốt sợi dây con lắc đơn M sẽ dao động với biên độ góc \(\alpha ={{\alpha }_{0}}=10,{{16}^{0}}\)
Vận tốc khi M qua vị trí cân bằng
\(v=\sqrt{2g\ell \left( 1-\cos {{\alpha }_{0}} \right)}=39,2~\text{cm}/\text{s}\)
Đề thi thử THPT QG năm 2021 môn Vật Lý
Trường THPT Quang Trung
.png)