Một con lắc đơn được treo vào trần 1 toa của đoàn tàu hỏa. Khi tàu đúng yên, con lắc dao động bé với chu kì T = 2s. Khi đoàn tàu này chuyển động với tốc độ không đổi v = 15 m/s trên 1 đường ray nằm trên mặt phẳng nằm ngang có dạng 1 cung tròn bán kính cong R = 400m. Cho biết gia tốc trọng trường là g = 10 m/s2, bán kính cong R rất lớn so với chiều dài con lắc và khoảng cách giữa 2 thanh ray. Bỏ qua mất mát năng lượng. Chu kì dao động nhỏ của con lắc khi đó gần giá trị nào nhất sau đây?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai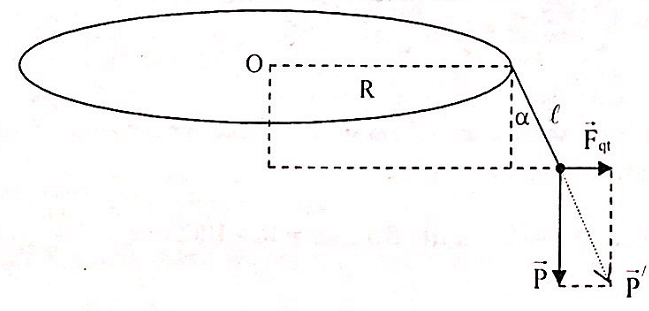
+ Vì xe chuyển động tròn đều nên xe chịu tác dụng của lực quán tính li tâm:
\({F_{qt}} = m{\omega ^2}\left( {R + \ell \sin \alpha } \right) = m\frac{{{v^2}}}{{\left( {R + \ell \sin \alpha } \right)}}\)
+ Vì R rất lớn so với
\(\begin{array}{l}
\ell \Rightarrow R > > \ell \sin \alpha \Rightarrow R + \ell \sin \alpha \approx R\\
\Rightarrow {F_{qt}} \approx m\frac{{{v^2}}}{R} \Rightarrow {g^/} = \sqrt {{g^2} + {{\left( {\frac{{{F_{qt}}}}{m}} \right)}^2}} \\
\Rightarrow {g^/} = \sqrt {{g^2} + {{\left( {\frac{{{v^2}}}{R}} \right)}^2}} = \sqrt {{g^2} + \left( {\frac{{{v^4}}}{{{R^2}}}} \right)}
\end{array}\)
+ Chu kì:
\(\begin{array}{l}
T = 2\pi \sqrt {\frac{\ell }{g}} \Rightarrow \frac{{{T^/}}}{T} = \sqrt {\frac{g}{{{g^/}}}} \\
\Rightarrow {T^/} = T\sqrt {\frac{g}{{\sqrt {{g^2} + \left( {\frac{{{v^4}}}{{{R^2}}}} \right)} }}} \approx 1,998\left( s \right)
\end{array}\)
Đề thi thử THPT QG năm 2021 môn Vật Lý
Trường THPT Trần Quốc Thảo
Câu hỏi liên quan
-
Một electron đang chuyển động với tốc độ v = 0,6c (c là tốc độ ánh sáng trong chân không). Nếu tốc độ của nó tăng lên 4/3 lần so với ban đầu thì động năng của electron sẽ tăng thêm một lượng:
-
Quang phổ liên tục phát ra bởi hai vật khác nhau thì:
-
Mạch dao động lý tưởng: C = 50 μF, L = 5 mH. Hiệu điện thế cực đại ở hai bản tụ là 6 (V) thì dòng điện cực đại chạy trong mạch là:
-
Tần số của dao động cưỡng bức:
-
Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng λ. Hai điểm M và N thuộc mặt nước, nằm trên hai phương truyền sóng mà các phần tử nước đang dao động. Biết OM = 8λ, ON = 12λ và OM vuông góc với ON. Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là:
-
Công thức tính tổng trở của đoạn mạch RLC mắc nối tiếp là
-
Ban đầu có N0 hạt phóng xạ X có chu kì bán rã T. Số hạt của chất X còn lại sau khoảng thời gian 3T, kể từ thời điểm ban đầu là:
-
Theo ND thuyết lượng tử ánh sáng, phát biếu nào dưới đây là sai?
-
Hai con lắc đơn có chiều dài lần lượt là l1 và l2, dao động tự do tại cùng một nơi trên Trái Đất với tần số tương ứng là f1 và f2. Biết l1=2l2, hệ thức nào sau đây là đúng ?
-
Khi nói về tia X, phát biểu nào sau đây sai?
-
Mạng điện dân dụng của Việt Nam đang dùng có tần số là:
-
Một chất điểm dddh không ma sát với biên độ A. Khi vừa qua khỏi vị trí cân bằng một đoạn s động năng của chất điểm là 1,8J. Đi tiếp một đoạn s nữa thì động năng chỉ còn 1,5J. Tỉ số s/A có giá trị gần nhất với giá trị nào sau đây:
-
Một dung dịch hấp thụ bức xạ có bước sóng λ1 và phát ra bức xạ có bước sóng λ2 (với λ1 = 1,5λ1). Người ta gọi hiệu suất của sự phát quang là tỉ số giữa năng lượng ánh sáng phát quang và năng lượng ánh sáng hấp thụ. Số phôtôn bị hấp thụ dẫn đến sự phát quang chiếm tỉ lệ là 1/5 của tổng số phôtôn chiếu tới dung dịch. Hiệu suất của sự phát quang của dung dịch là:
-
Biến điệu sóng điện từ là:
-
Biết khối lượng của hạt nhân neon Ne20, hạt α, của proton và nơtron lần lượt là mNe = 19,9870u, mα = 4,0015u, mp = l,0073u, mn = l,0087u. Hãy so sánh độ bền của hạt α và hạt neon.
-
Một đám nguyên tử hidro đang ở trạng thái kích thích mà electron chuyển động trên quỹ đạo dừng N. Khi electron chuyển về các quỹ đạo dừng bên trong thì quang phổ vạch phát xạ của đám nguyên tử đó có bao nhiêu vạch?
-
Từ thông xuyên qua một khung dây dẫn phẳng biến thiên điều hòa theo thời gian theo quy luật ϕ = ϕ0cos(ωt + φ1) làm cho trong khung dây xuất hiện một suất điện động cảm ứng e = E0cos(ωt + ϕ2). Hiệu φ2 – φ1 nhận giá trị là:
-
Một con lắc lò xo dddh với biên độ A = 10cm. Đồ thị biểu thị mối liên hệ giữa động năng và vận tốc của vật dao động được cho như hình bên.
Chu kì và độ cứng của lò xo lần lượt là:
-
Tại mặt chất lỏng có hai nguồn phát sóng kết hợp A, B cách nhau 16 cm, đao động điều hòa theo phương vuông góc với mặt chất lỏng với phương trình uA = 2cos(40πt) cm và uB = 2cos(40πt + π) cm. Tốc độ truyền sóng trên mặt chất lỏng là 40 cm/s. Gọi M là một điểm thuộc mặt chất lỏng, nằm trên đường thẳng Ax vuông góc với AB, cách A một đoạn ngắn nhất mà phần tử chất lỏng tại M dao động với biên độ cực đại. Khoảng cách AM bằng bao nhiêu?
-
Hãy chọn câu đúng. Công thức liên hệ giữa tốc độ sóng v, bước sóng λ, chu kì T và tần số f của sóng:
