Một con lắc đơn gồm vật nhỏ \(m\) treo ở đầu sợi dây không dãn có khối lượng không đáng kể dao động điều hòa tại nơi có \(g = 10\,\,m/{s^2}\). Người ta tích điện cho vật \(m\) và đặt con lắc vào trong một điện trường đều nằm ngang thì chu kì dao động là \(T\). Nếu quay phương của điện trường trong mặt phẳng thẳng đứng đi một góc \({30^0}\) so với phương ngang thì chu kì dao động của con lắc bằng \(1,987\,\,s\) hoặc \(1,147\,\,s\). Giá trị của chu kì \(T\) bằng
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiNhận xét: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \Rightarrow {T^2} = 4{\pi ^2}\dfrac{{\rm{l}}}{g} \Rightarrow {T^2} \sim \dfrac{1}{g}\) hay \(g \sim \dfrac{1}{{{T^2}}}\)
Ban đầu \(\overrightarrow F \) theo phương ngang, gia tốc hiệu dụng: \({g_0} = \sqrt {{g^2} + {a^2}} \)
Trường hợp 1: \(\overrightarrow F \) hướng lên trên
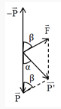
Ta có: \(\beta = {90^0} - \alpha \Rightarrow \cos \beta = - \sin \alpha \)
Gia tốc hiệu dụng là: \({g_1} = \sqrt {{g^2} + {a^2} + 2g.a.\sin \alpha } \Rightarrow {g_1}^2 = {g^2} + {a^2} + 2g.a.\sin \alpha \,\,\left( 1 \right)\)
Trường hợp 2: \(\overrightarrow F \) hướng xuống dưới:
.jpg)
Ta có: \(\beta = {90^0} + \alpha \Rightarrow \cos \beta = \sin \alpha \)
Gia tốc hiệu dụng là: \({g_2} = \sqrt {{g^2} + {a^2} - 2g.a.\sin \alpha } \Rightarrow {g_2}^2 = {g^2} + {a^2} - 2g.a.\sin \alpha \,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \({g_1}^2 + {g_2}^2 = 2\left( {{g^2} + {a^2}} \right)\)
\( \Rightarrow \dfrac{1}{{{T_1}^4}} + \dfrac{1}{{{T_2}^4}} = \dfrac{2}{{{T_0}^4}} \Rightarrow \dfrac{1}{{1,{{987}^4}}} + \dfrac{1}{{1,{{147}^4}}} = \dfrac{2}{{{T_0}^4}} \Rightarrow {T_0} \approx 1,329\,\,\left( s \right)\)
Chọn B.
Đề thi thử THPT QG năm 2022 môn Vật Lý
Trường THPT Lý Chính Thắng
.jpg)
.jpg)











