Một con lắc lò xo treo thẳng đứng đang dao động điều hòa. Đồ thị (1) biểu diễn lực hồi phục phụ thuộc vào thời gian. Đồ thị (2) biểu diễn độ lớn lực đàn hồi phụ thuộc vào thời gian. Lấy g = π2 m/s2 . Phương trình dao động của vật là
.jpg)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTừ đồ thị ta có tỉ số: \(\frac{1}{2}=\frac{kA}{k(A-\Delta l)}\Rightarrow \Delta l=\frac{A}{2}\)
Tại thời điểm 1/6 s \({{F}_{kv}}=-kx=1N\Rightarrow x=-\frac{A}{2}\) đang tiến về vị trí cân bằng
lúc t = 0 x = 0 và đang đi theo chiều âm (vì Fkv đang tăng). Như vậy từ lúc t = 0 đến t = 1.6 s ứng với: T/4 + T/6 = 1/6 s
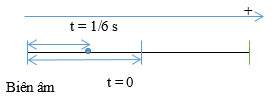
\(\Rightarrow T=0,4s\Rightarrow \left\{ \begin{align} & \Delta l=4cm\to A=8cm \\ & \omega =5\pi (rad/s) \\ \end{align} \right.\)
lúc t = 0 x = 0 và đang đi theo chiều âm \(\phi =\frac{\pi }{2}\)
Vậy \(x=8\cos \left( 5\pi t+\frac{\pi }{2} \right)cm\)

.jpg)
.jpg)











