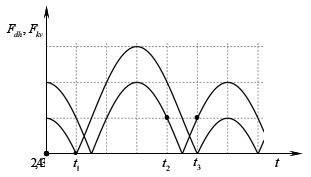
Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có \(g=10\,\,\text{m/}{{\text{s}}^{\text{2}}}\text{.}\) Hình bên là đồ thị biểu diễn sự phụ thuộc của độ lớn lực kéo về \({{F}_{kv}}\) tác dụng lên vật và độ lớn lực đàn hồi \({{F}_{dh}}\) của lò xo theo thời gian t. Biết \({{t}_{2}}-{{t}_{1}}=\frac{\pi }{20}\,\)s. Tốc độ của vật tại thời điểm \(t={{t}_{3}}\) gần nhất giá trị nào sau đây?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:
\({{\left( \frac{{{F}_{dh}}}{{{F}_{kv}}} \right)}_{max}}=\frac{A+\Delta {{l}_{0}}}{A}=\frac{3}{2}\) → \(A=2\Delta {{l}_{0}}\).
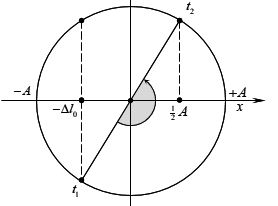
\(t={{t}_{1}}\) thì \({{F}_{dh}}=0\) → vật đi qua vị trí lò xo không biến dạng, \({{x}_{1}}=-\Delta {{l}_{0}}\).
\(t={{t}_{2}}\) thì \({{F}_{kv}}=\frac{1}{2}{{F}_{kvmax}}\) → vật đi qua vị trí cân bằng, \({{x}_{2}}=+\frac{1}{2}A\).
\(\Delta t=\frac{T}{2}=\frac{\pi }{20}\)s → \(T=\frac{\pi }{10}\)s → \(\omega =20\) rad/s → \(\Delta {{l}_{0}}=2,5\)cm và \(A=5\) cm.
\(t={{t}_{3}}\) thì \({{F}_{dh}}=0\) → \(x=-\Delta {{l}_{0}}=-2,5\)cm
→ \(v=\frac{\sqrt{3}}{2}{{v}_{max}}=\frac{\sqrt{3}}{2}\left( 5.20 \right)\approx 87\)cm/s.