Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
.png)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTừ đồ thị ta thấy biên độ dao động: \(A=4cm\)
Ở thời điểm đầu, vật có li độ \(x=-2cm=-\frac{A}{2}\) và đang tăng
Ta có VTLG:
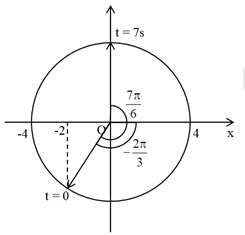
Từ đồ thị ta thấy pha đàu của dao động là: \(\varphi =-\frac{2\pi }{3}\left( rad \right)\)
Ở thời điểm \(t=7s\), vật ở VTCB và đang giảm → pha dao động là: \(\frac{\pi }{2}\left( rad \right)\)
Góc quét từ thời điểm \(t=0\) đến \(t=7s\) là: \(\Delta \varphi =\frac{\pi }{2}-\left( -\frac{2\pi }{3} \right)=\frac{7\pi }{6}\left( rad \right)\)
Tần số góc của dao động là: \(\omega =\frac{\Delta \varphi }{\Delta t}=\frac{\frac{7\pi }{6}}{7}=\frac{\pi }{6}\left( rad/s \right)\)
Phương trình dao động của vật là: \(x=4\cos \left( \frac{\pi }{6}t-\frac{2\pi }{4} \right)\left( cm \right)\)
.png)











