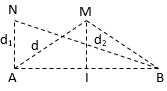
Tại hai điểm A và B trên mặt nước cách nhau 16 cm có hai nguồn giống nhau. Điểm M nằm trên mặt nước và nằm trên đường trung trực của AB, cách trung điểm I của AB một khoảng nhỏ nhất bằng 4\(\sqrt{5}\)cm luôn dao động cùng pha với I. Điểm N nằm trên mặt nước và nằm trên đường thẳng vuông góc với AB tại A, cách A một khoảng nhỏ nhất bằng bao nhiêu để N dao động với biên độ cực tiểu?

Câu hỏi liên quan

• Nếu chiếu một chùm tia hồng ngoại vào tấm kẽm tích điện âm, thì

• Hai sóng cùng tần số, được gọi là sóng kết hợp, nếu có

• Phát biểu nào sau đây là đúng khi nói về phản ứng hạt nhân?

ZUNIA12

• Đặt điện áp u = U₀cos100πtV vào hai đầu đoạn mạch A, B gồm cuộn dây thuần cảm, có độ tự cảm \(L=\frac{1}{4\pi }H\) và tụ có điện dung \(C=\frac{400}{3\pi }\mu F\) mắc nối tiếp. Tại thời điểm điện áp tức thời giữa hai đầu tụ điện bằng 120 V thì điện áp tức thời giữa hai đầu A, B có giá trị bằng

• Một vật nhỏ dao động điều hòa theo một trục cố định. Phát biểu nào sau đây đúng?

• Điện năng từ nhà máy được đưa tới nơi tiêu thụ nhờ các dây dẫn. Biết công suất truyền đi là không đổi. Ban đầu hiệu suất truyền tải điện là 80%. Muốn hiệu suất truyền tải điện là 85% thì cần giảm cường độ dòng điện trên dây tải đi

• Một con lắc lò xo nằm ngang gồm vật nặng M = 200 g và độ cứng lò xo k = 40 N/m có thể trượt không ma sát trên mặt phẳng nằm ngang. Khi hệ đang ở trạng thái cân bằng thì có một vật khối lượng m = 200 g chuyển động đến va chạm mềm vào M theo phương ngang với tốc độ 3 m/s. Sau va chạm hệ dao động điều hòa với biên độ là

   

• Một đoạn mạch xoay chiều gồm cuộn dây thuần cảm L = 1/p (H) mắc nối tiếp với R = 100W. Hiệu điện thế ở hai đầu mạch là u = 100\(\sqrt{2}\)sin100pt (V). Biểu thức cường độ dòng điện trong mạch là 

• Trong các ánh sáng đơn sắc sau đây. Ánh sáng nào có khả năng gây ra hiện tượng quang điện mạnh nhất?

• Một mạch chọn sóng của máy thu có cuộn cảm L=2mH và tụ điện có điện dung biến thiên từ 4pF đến 7pF. Như vậy máy thu không thể nhận được các đài phát sóng có tần số

• Trên vỏ của một acquy có ghi 12V, điện trở trong của acquy là 0,06\(\Omega \). Mắc vào hai cực của acquy một bóng đèn có ghi 12V – 5W. Khi đó, cường độ dòng điện chạy qua đèn là

• Đặt vào hai đầu đoạn mạch RLC nối tiếp một hiệu điện thế xoay chiều u = U_o sinωt thì độ lệch pha của hiệu điện thế u với cường độ dòng điện i trong mạch được tính theo công thức

• Có 100 (g) chất phóng xạ với chu kì bán rã là 7 ngày đêm. Sau 28 ngày đêm khối lượng chất phóng xạ đó còn lại là

• Hạt nhân \({}_{92}^{238}U\) có cấu tạo gồm

• Một vật dao động điểu hòa khi đang chuyển động từ vị trí cân bằng đến vị trí biên âm thì

• Một sóng ngang có chu kì T = 0,2 s truyền trong một môi trường đàn hồi có tốc độ 1 m/s. Xét trên phương truyền sóng Ox, vào một thời điểm nào đó một điểm M nằm tại đỉnh sóng thì ở sau M theo chiều truyền sóng, cách M một khoảng từ 42 cm đến 60 cm có điểm N đang từ vị tri cân bằng đi lên đỉnh sóng. Khoảng cách MN là:

• Cho ba điện tích q₁= 4µC, q₂= 16µC, q₃ = - 64µC lần lượt đặt tại ba điểm A,B,C thẳng hàng( trong chân không). Biết AB=20cm, BC=60cm. Lực điện tổng hợp tác dụng lên điện tích q₁ bằng:

• Quang phổ Mặt Trời được máy quang phổ ghi được là:

• Lần lượt chiếu hai bức xạ có bước sóng λ₁ = 0,75 μm và λ₂ = 0,25 μm vào một tấm kẽm có giới hạn quang điện λ_o = 0,35 μm. Bức xạ nào gây ra hiện tượng quang điện ?

• Khi một hạt nhân nguyên tử phóng xạ lần lượt một tia α và một tia β^– thì hạt nhân nguyên tử sẽ biến đổi như thế nào ?