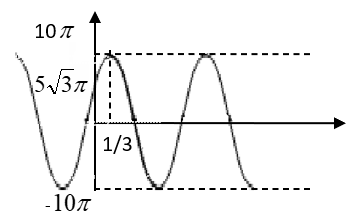
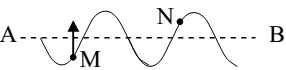
Thí nghiệm giao thoa I-âng với ánh sáng đơn sắc có bước sóng là 0,6 um, khoảng cách giữa hai khe a=1mm, khoảng cách hai khe đến màn D= 2 m. Màn ảnh giao thoa có khối lượng 200g gắn với một lò xo nằm ngang có độ cứng là k, sao cho màn có thể dao động không ma sát theo phương ngang trùng với trục của lò xo và vuông góc với mặt phăng hai khe (hình vẽ). Tại thời điểm t = 0 (màn ở vị trí cân bằng), truyền cho màn một vận tốc ban đầu hướng về phía hai khe để màn dao động điều hòa với biên độ 40cm. Thời gian từ lúc màn dao động đến khi điểm M trên màn cách vân trung tâm b = 8 mm cho vân tối lần thứ 4 là 0,4s. Độ cứng k của lào xo là

Câu hỏi liên quan

• Mạch dao động điện từ tự do LC gồm cuộn dây thuần cảm L và tụ điện có điện dung C = 4μF. Điện tích trên bản tụ biến thiên điều hòa theo biểu thức:\(q={{0,2.10}^{-3}}.Cos(500\pi t+\frac{\pi }{6})\)C. Giá trị hiệu điện thế giữa hai đầu bản tụ điện vào thời điểm t = 3ms là:

• Hai dao động điều hòa với phương trình sau: x₁ = A₁ cos(4\(\pi \)t \(-\frac{\pi }{6}\)) cm, x₂ = A₂cos(4\(\pi \)t +\(\frac{\pi }{2}\)) cm. Biết A_TH=\(\sqrt{3}\)cm. Để A₁ cực đại thì A₂ bằng bao nhiêu?

• Đặt điện áp u = U₀coswt (U₀ không đổi, ω thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C (với R, L, C không đổi). Khi thay đổi ω để công suất điện tiêu thụ của đoạn mạch đạt giá trị cực đại thì hệ thức đúng là:

ZUNIA12

• Một sóng truyền theo phương AB. Tại một thời điểm nào đó, hình dạng sóng có dạng như hình vẽ. Biết rằng điểm M đang đi lên vị trí cân bằng. Khi đó điểm N đang chuyển động:

  

• Pôlôni(²¹⁰₈₄Po) là chất phóng xạ, phát ra hạt  α và biến thành hạt nhân Chì (Pb). Po có chu kì bán rã là 138 ngày. Ban đầu có 1kg chất phóng xạ trên. Sau bao lâu lượng chất trên bị phân rã 968,75g

• Trong một mạch kín dòng điện cảm ứng xuất hiện khi

• Cho mạch điện xoay chiều gồm cuộn dây mắc nối tiếp với  biến trở R. Hiệu điện thế có giá trị hiệu dụng và tần số không đổi. Đồ thị công suất toàn mạch phụ thuộc vào R như hình. Cuộn dây có tổng trở là:

  

• Về sóng cơ học, phát biểu nào sau đây sai?

• Điện gồm R, L và C theo thứ tự nối tiếp, cuộn dây có điện trở r. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số f = 50 Hz. Cho điện dung C thay đổi người ta thu được đồ thị liên hệ giữa điện áp hiệu dụng hai đầu mạch chứa cuộn dây và tụ điện U_rLC với điện dung C của tụ điện như hình vẽ bên. Điện trở r có giá trị bằng

  

• Vật dao động điều hòa với đồ thị vận tốc theo thời gian như hình vẽ. Phương trình nào sau đây sẽ có mối liên hệ chính xác với đồ thi vận tốc  ?

  

• Đoạn mạch R – L – C mắc nối tiếp. Biết rằng \({{U}_{L}}=\frac{1}{2}{{U}_{C}}\) . So với dòng điện i thì điện áp u ở hai đầu mạch sẽ:

• Nguồn âm S phát ra một âm có công suất P không đổi, truyền đẳng hướng về mọi phương. Tại điểm A cách S một đoạn 1m, mức cường độ âm là 70 dB. Giả sử môi trường không hấp thụ âm. Mức cường độ âm tại điểm B cách nguồn một đoạn 10 m là

• Tại một điểm trên trái đất có sóng điện từ truyền qua.Tại đó véc tơ cảm ứng từ \(\vec{B}\) hướng thẳng đứng từ dưới lên, véc tơ cường độ điện trường \(\vec{E}\) nằm ngang hướng từ Đông sang Tây.Sóng điện từ truyền theo chiều

• Khối lượng của hạt nhân ⁹₄Be là 9,0027u, khối lượng của nơtron là m_n = 1,0086u, khối lượng của prôtôn là m_p = 1,0072u. Độ hụt khối của hạt nhân ⁹₄Be là

• Cho mạch xoay chiều có R, L, C mắc nối tiếp cho R=30ôm ,L = \(\frac{1}{\pi }\)(F). C thay  đổi, hiệu điện thế 2 đầu mạch là  u=120\(\sqrt{2}\)cos100\(\pi \)t (V)  với C bằng bao nhiêu thì u,i cùng pha. Tìm P khi đó

• Một sợi dây bạch kim ở nhiệt độ 20⁰C có điện trở suất là \({{\rho }_{0}}={{10,6.10}^{-8}}\Omega m\). Biết hệ số nhiệt điện trở của bạch kim là \(\alpha ={{3,9.10}^{-3}}{{K}^{-1}}\). Điện trở suất \(\rho \)của sợi dây bạch kim ở 500⁰C là:

• Mức năng lượng trong nguyên tử hiđrô được xác định bằng: \(E=-\frac{13,6}{{{n}^{2}}}\left( eV \right)\), trạng thái cơ bản ứng với n = 1. Khi nguyên tử chuyển từ mức năng lượng O về N thì phát ra một phôtôn có bước sóng λ₀. Khi nguyên tử hấp thụ một phôtôn có bước sóng λ nó chuyển từ mức năng lượng K lên mức năng lượng M. So với λ₀ thì λ

• Một vật nhỏ dao động điều hòa theo phương trình \(x=A\cos \left( 10t \right)\)(t tính bằng s). Tại t= 2 s, pha của dao động là

• Định luật Cu-lông được áp dụng cho trường hợp tương tác nào sau đây? Hai điện tích điểm:

• Hai tấm kim loại phẳng song song cách nhau 2cm nhiễm điện trái dấu. Muốn làm cho điện tích q=5.10^-10C di chuyển từ tấm này sang tấm kia cần tốn một công A=2.10^-9J. Xác định cường độ điện trường bên trong hai tấm kim loại, biết điện trường bên trong là điện trường đều có đường sức vuông góc với các tấm.