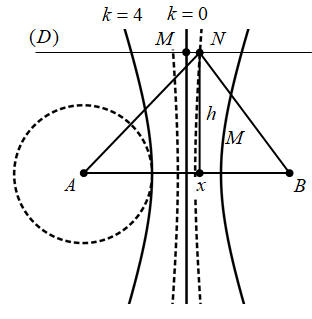
Trong thí nghiệm giao thoa sóng mặt nước, hai nguồn kết hợp \(A\), \(B\) cách nhau 8 cm dao động cùng pha. Ở mặt nước, có 21 đường dao động với biên độ cực đại và trên đường tròn tâm \(A\) bán kính 2,5 cm có 13 phần tử sóng dao động với biên độ cực đại. Đường thẳng (\(D\)) trên mặt nước song song với \(AB\) và cách đường thẳng \(AB\) một đoạn 5 cm. Đường trung trực của \(AB\) trên mặt nước cắt đường thẳng (\(D\)) tại \(M\). Điểm \(N\) nằm trên (\(D\)) dao động với biên độ cực tiểu gần \(M\) nhất cách \(M\) một đoạn \(d\). Giá trị \(d\) gần nhất với giá trị nào sau đây?

Câu hỏi liên quan

• Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có \(g=10\,\,\text{m/}{{\text{s}}^{\text{2}}}\text{.}\) Hình bên là đồ thị biểu diễn sự phụ thuộc của độ lớn lực kéo về \({{F}_{kv}}\) tác dụng lên vật và độ lớn lực đàn hồi \({{F}_{dh}}\) của lò xo theo thời gian \(t.\) Biết \({{t}_{2}}-{{t}_{1}}=\frac{\pi }{20}\,\)s. Gia tốc của vật tại thời điểm \(t={{t}_{3}}\) có độ lớn gần nhất giá trị nào sau đây?

  

• Một sợi dây đang có sóng dừng ổn định. Sóng truyền trên dây có chu kì \(T=0,1\pi \)s, biên độ của bụng là 4 cm. Với hai bụng liên tiếp trên dây, khi vận tốc tương đối giữa chúng có độ bằng 160 cm/s thì kết luận nào sau đây là đúng?

• Đặt điện áp xoay chiều \(u=U\sqrt{2}\cos \omega t\,\,\left( \omega >0 \right)\) vào hai đầu một cuộn cảm thuần \(L\) thì cường độ dòng điện qua mạch được xác định bằng biểu thức

ZUNIA12

• Chất quang dẫn sẽ trở nên dẫn điên tốt nếu

• Trên một sợi dây có hai đầu cố định, đang có sóng dừng với biên độ dao động của bụng sóng là 4 cm. Khoảng cách giữa hai đầu dây là 60 cm, sóng truyền trên dây có bước sóng là 30 cm. Gọi \(M\) và \(N\) là hai điểm trên dây mà phần tử tại đó dao động với biên độ lần lượt là \(2\sqrt{2}\) cm và 2 cm. Gọi \({{d}_{max}}\) là khoảng cách lớn nhất giữa \(M\) và \(N\), \({{d}_{\min }}\) là khoảng cách nhỏ nhất giữa \(M\) và \(N\). Tỉ số \(\frac{{{d}_{max}}}{{{d}_{\min }}}\) có giá trị gần nhất với giá trị nào sau đây? 

  

• Trong chân không, các bức xạ có bước sóng tăng dần theo thứ tự đúng là

• Một con lắc đơn dao động theo phương trình \(s=4\cos \left( 2\pi t \right)\,\)cm (\(t\) tính bằng giây). Quãng đường mà con lắc này đi được trong khoản thời gian \(\Delta t=\frac{1}{3}\)s là

• Cho đoạn mạch \(RLC\) mắc nối tiếp với \(R=60\)Ω, \(L=0,8\)H, \(C\) có thể thay đổi được. Ta đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u=120\cos \left( 100t+\frac{\pi }{2} \right)\)V, thay đổi \(C\) đến khi điện áp hiệu dụng ở hai đầu điện trở là cực đại. Điện áp giữa hai bản tụ khi đó là

• Đặt điện áp xoay chiều \(u={{U}_{0}}\cos \omega t\,\,\left( {{U}_{0}}>0 \right)\) vào hai đầu một đoạn mạch có \(R,\,\,L,\,\,C\) mắc nối tiếp thì trong đoạn mạch có cộng hưởng điện. Nếu ta tăng chu kì của dòng điện, đồng thời giữ nguyên các thông số còn lại. Kết luận nào sau đây là sai?

• Đặt một điện áp xoay chiều vào hai đầu một đoạn mạch gồm điện trở \(R=40\) mắc nối tiếp với cuộn cảm thuần có cảm kháng \({{Z}_{L}}=30\)Ω. Độ lệc pha giữa điện áp và dòng điện trong mạch điện xoay chiều này bằng 

• Trong chân không, ánh sáng nhìn thấy có bước sóng nằm trong khoảng từ 0,38 μm đến 0,76 μm. Cho biết: hằng số P – lang \(h=6,{{625.10}^{-34}}\)Js, tốc độ ánh sáng trong chân không \(c={{3.10}^{8}}\)m/s và \(1eV=1,{{6.10}^{-19}}\)J. Các photon của ánh sáng này có năng lượng nằm trong khoảng

• Năng lượng liên kết tính trên một nucleon của hạt nhân \({}_{Z}^{A}X\) được xác định bằng biểu thức nào sau đây? Biết khối lượng của proton, notron và hạt nhân lần lượt là \({{m}_{p}},{{m}_{n}},{{m}_{X}}\).

• Một nguyên tử đang ở trạng thái trung hòa về điện thì nhận thêm hai electron. Điện tích của nguyên tử sau đó bằng 

• Âm sắc là đặc trưng sinh lý của âm gắn liền với

• Tại nơi có gia tốc trọng trường \(g\), một con lắc đơn có chiều dài \(l\) dao động điều hòa. Chu kì biến đổi của thế năng bằng

• Một máy biến áp lí tưởng cung cấp công suất 4 kW có điện áp hiệu dụng ở đầu cuộn thứ cấp là 220 V. Nối hai đầu cuộn thức cấp với đường dây tải điện có điện trở bằng 2 Ω. Điện áp hiệu dụng ở cuối đường dây tải điện là

• Khi một sóng điện từ có tần số \({{2.10}^{6}}\)Hz truyền trong một môi trường với tốc độ \(2,{{25.10}^{8}}\) m/s thì có bước sóng là

• Cho mạch điện không đổi như hình vẽ. Mạch ngoài chứa điện trở \(R\), nguồn có suất điện động \(\xi \) và điện trở trong \(r\). Hiệu điện thế giữa hai điểm \(M\) và \(N\) được xác định bằng biểu thức nào sau đây?

  

• Dùng thí nghiệm Y − âng về giao thoa ánh sáng. Khoảng vân đó đo được trên màn là 1,6 mm. Vị tí của vân sáng bậc 4 trên màn quan sát cách vân trung tâm một khoảng

• Khi nói về tia Rơn – ghen và tia tử ngoại, phát biểu nào sau đây sai?