Trong thí nghiệm giao thoa sóng với hai nguồn kết hợp A, B trên mặt nước, dao động cùng pha. Xét hai điểm C, D thuộc đường thẳng Ay vuông góc với AB tại A, với CA = 9 cm, DA = 16 cm. Dịch chuyển nguồn B dọc theo đường thẳng chứa AB đến khi góc CBD là lớn nhất thì thấy C và D thuộc hai cực đại giao thoa liền kề. Gọi M là điểm nằm trên Ay dao động với biên độ cực tiểu. Giá trị lớn nhất của AM là
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có hình vẽ:
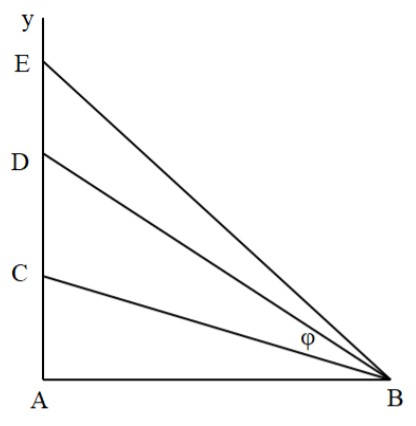
Để \(CB{{D}_{\max }}\Rightarrow {{\alpha }_{\max }}\Rightarrow {{(\tan \alpha )}_{\max }}\)
Xét \(\tan \alpha =\tan (ABD-ABC)=\frac{\tan ABD-\tan ABC}{1+\tan ABD\tan ABC}\)
\(\Rightarrow \tan \alpha =\frac{\frac{AD}{AB}-\frac{AC}{AB}}{1+\frac{AD}{AB}\cdot \frac{AC}{AB}}=\frac{AD-AC}{AB+\frac{AD.AC}{AB}}=\frac{7}{AB+\frac{144}{AB}}\)
Để \({{(\tan \alpha )}_{\max }}\Rightarrow {{\left( AB+\frac{144}{AB} \right)}_{\min }}\)
Áp dụng bất đẳng thức Cô – si, ta có:
\(AB+\frac{144}{AB}\ge 2\sqrt{AB\cdot \frac{144}{AB}}\Rightarrow {{\left( AB+\frac{144}{AB} \right)}_{\min }}\Leftrightarrow AB=12(cm)\)
AB AB AB Tại C, D là hai cực đại liên tiếp
→ D là cực đại bậc k, C là cực đại bậc (k+1), ta có:
\(\left\{ \begin{array}{*{35}{l}} DB-DA=\sqrt{D{{A}^{2}}+A{{B}^{2}}}-DA=k\lambda \Rightarrow k\lambda =4 \\ CB-CA=\sqrt{C{{A}^{2}}+A{{B}^{2}}}-CA=(k+1)\lambda \Rightarrow (k+1)\lambda =6 \\ \end{array}\Rightarrow \lambda =2(cm) \right.\)
Xét điểm E là cực tiểu xa A nhất → E là cực tiểu bậc 1 (k = 0)
Ta có:
\(EB-EA=\frac{1}{2}\lambda \Rightarrow \sqrt{E{{A}^{2}}+A{{B}^{2}}}-EA=\frac{1}{2}\lambda \)
\(\Rightarrow \sqrt{E{{A}^{2}}+{{12}^{2}}}-EA=1\Rightarrow EA=71,5(cm)\)
Chọn D.
Đề thi thử THPT QG năm 2022 môn Vật Lý
Trường THPT Nguyễn Duy Hiệu
.jpg)
.jpg)
.jpg)
.jpg)