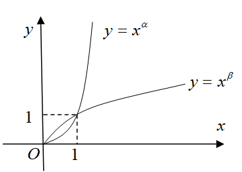
Cho \(\alpha \),\(\beta \) là các số thực. Đồ thị các hàm số sau \(y={{x}^{\alpha }}\),\(y={{x}^{\beta }}\) trên khoảng \(\left( 0;+\infty \right)\) được cho trong hình. Khẳng định nào đúng?
Chính xác
Xem lời giải
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Chủ đề: Đề thi THPT QG
Môn: Toán
Lời giải:
Báo saiVới x0 > 1 ta có:
\(\begin{align} & x_{0}^{\alpha }>1\Rightarrow \alpha >0;x_{0}^{\beta }>1\Rightarrow \beta >0 \\ & x_{0}^{\alpha }>x_{0}^{\beta }\Rightarrow \alpha >\beta \\ \end{align}\)
Mặt khác, dựa vào hình dáng đồ thị ta suy ra \(\alpha >1\) và \(\beta <1\).
\(\Rightarrow 0<\beta <1<\alpha \)
Chọn D
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề thi thử Tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Phú Lâm
26/12/2024
63 lượt thi
0/50
Bắt đầu thi
ADMICRO
YOMEDIA
ZUNIA9
.PNG)
.PNG)











