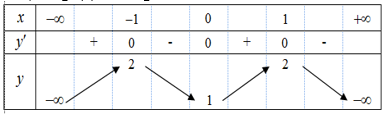
Cho HS \(y=f(x)\) có đạo hàm trên \(\mathbb{R}\), thỏa mãn \(f(2) \leq f(-2)=2020\). Hàm số \(y={f}'(x)\) có đồ thị như hình:

Hàm số \(g(x)=[2020-f(x)]^2\) nghịch biến trên khoảng?

Câu hỏi liên quan

• Cho hàm số \(y=f(x)\) liên tục trên \(R\) và có đồ thị như hình. Có bao nhiêu giá trị nguyên của tham số \(m\)để phương trình \(f\left( f(\cos x) \right)=m\) có nghiệm thuộc khoảng \(\left( \frac{\pi }{2};\frac{3\pi }{2} \right)?\)

  

• Cho cấp số cộng sau \(\left( {{u}_{n}} \right)\) có số hạng đầu \({{u}_{1}}=3\) và công sai \(d=2\). Giá trị của \({{u}_{7}}\) bằng?

• Cho hàm số \(y=f\left( x \right)\) có BBT như sau:

  

  Hàm số \(y=f\left( x \right)\)đồng biến trên khoảng nào dưới đây? 

ZUNIA12

• Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), biết \(AB=a,\,\,AC=2a\). Mặt bên \(\left( SAB \right)\) là tam giác đều và nằm trong mp vuông góc với đáy. Tính theo \(a\) thể tích khối chóp \(S.ABC\)?

• Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(2a,\) cạnh bên bằng \(3a\). K/c từ \(A\) đến mặt phẳng \(\left( SCD \right)\) bằng?

• Cho hình nón có chiều cao bằng \(8\,\text{cm}\), bán kính đáy bằng \(6\,\text{cm}\). Diện tích toàn phần Stp của hình nón đã cho bằng?

• Cho \(a\) là số thực dương. Tính giá trị của biểu thức \(P={{a}^{\frac{2}{3}}}\sqrt{a}\) bằng?

• Cho hình hộp đứng \(ABCD.{A}'{B}'{C}'{D}'\) có đáy \(ABCD\) là hình thoi có cạnh là \(a\), \(\widehat{BAD}=120{}^\circ \). Gọi \(G\) là trọng tâm tam giác \(ABD\), góc tạo bởi \({C}'G\) với mặt phẳng đáy bằng \(30{}^\circ \). Thể tích khối hộp \(ABCD.{A}'{B}'{C}'{D}'\) là?

• Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình:

  

  Giá trị cực tiểu của hàm số là?

• Có bao nhiêu số nguyên \(x\in \left[ -2022;2022 \right]\) thỏa mãn rằng \(\left( {{3}^{{{x}^{2}}}}-{{27}^{x}} \right)\sqrt{{{\log }_{2}}\left( 4x \right)-2}\ge 0\)?

• Người ta thả 2 quả cầu sắt có cùng bán kính \(r\) vào một chiếc hộp hình trụ đựng đầy nước sao cho các quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ (tham khảo hình vẽ). Biết lượng nước trong hộp ban đầu là \(12\) lít, hỏi lượng nước còn lại sau khi thả hai quả cầu là bao nhiêu? 

  

• Tổng tất cả các nghiệm của phương trình sau \({{3}^{2x}}-{{4.3}^{x}}+3=0\) bằng?

• Số nghiệm thực của phương trình sau \(3{{\log }_{3}}\left( 2x-1 \right)-{{\log }_{\frac{1}{3}}}{{\left( x-5 \right)}^{3}}=3\) là?

• Cho hàm số \(y=f\left( x \right)\). ĐTHS đạo hàm \(y={f}'\left( x \right)\) như hình vẽ bên. Đặt \(h\left( x \right)=3f\left( x \right)-{{x}^{3}}+3x\). Tìm mệnh đề đúng trong các mệnh đề sau? 

• Một người gửi số tiền \(500\) triệu đồng vào ngân hàng với lãi suất \(6,5%\)/năm theo hình thức lãi kép. Đến hết năm thứ \(3\), vì cần tiền nên người đó đến rút ra \(100\) triệu đồng, phần còn lại vẫn tiếp tục gửi. Hỏi sau \(5\) năm kể từ lúc bắt đầu gửi, người đó có được số tiền gần với số nào nhất dưới đây? 

• Thể tích \(V\) của khối cầu có bán kính \(R=a\sqrt{3}\) là?

• Đồ thị của hàm số nào dưới đây có dạng đường cong như hình?

  

• Trong bốn hàm số được liệt kê ở bốn phương án \(\text{A, B, C, D}\) dưới đây, hàm số nào bên dưới có bảng biến thiên sau?

  

• Cho hàm số bậc 4 \(y=f(x)\) có đồ thị hàm số \(y={f}'\left( x \right)\) như hình. Hàm số \(g\left( x \right)=4f\left( {{x}^{2}}-4 \right)+{{x}^{4}}-8{{x}^{2}}\) có bao nhiêu điểm cực tiểu?

  

• Tập nghiệm \(S\) của bất phương trình sau \({{\log }_{2}}\left( x-1 \right)<3\) là?