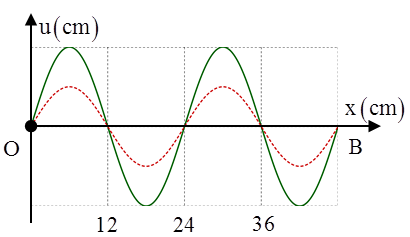
Trên một sợi dây OB căng ngang, hai đầu cố định, đang có sóng dừng với tần số f xác định. Gọi M, N và P là ba điểm trên dây có vị trí cân bằng cách B lần lượt là 4 cm, 6 cm và 38 cm. Hình vẽ mô tả hình dạng của sợi dây ở thời điểm t1 (nét liền) và thời điểm \({{t}_{2}}={{t}_{1}}+\frac{11}{12f}\) (nét đứt). Tại thời điểm t1, độ lớn li độ của phần tử dây ở N bằng biên độ của phần tử dây ở M và tốc độ của phần tử dây ở M là 60 cm/s. Tại thời điểm t2, vận tốc của phần tử dây ở P là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDựa vào đồ thị, ta có λ = 24 cm.
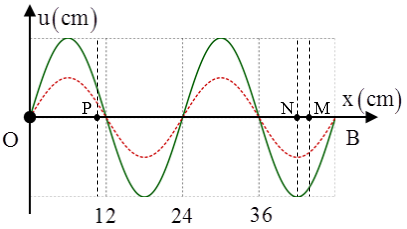
Ta có hình vẽ như bên (hình 1).
Ta có điểm M cách bụng sóng (điểm N) một khoảng \(\frac{\lambda }{12}\) nên có biên độ dao động là \({{A}_{M}}=\frac{A\sqrt{3}}{2}\) (với A là biên độ dao động của bụng sóng).
Ta có điểm P cách nút sóng một khoảng \(2\text{ }cm=\frac{\lambda }{12}\Rightarrow \) điểm P dao động với biên độ \({{A}_{P}}=\frac{A}{2}.\)
Ta có điểm M và N dao động cùng pha nên: \(\frac{{{u}_{M}}}{{{u}_{N}}}=\frac{\sqrt{3}}{2}\Rightarrow {{u}_{M}}=\frac{\sqrt{3}}{2}.{{u}_{N}}.\)
Ta có điểm M và P dao động ngược pha nên: \(\frac{{{u}_{M}}}{{{u}_{P}}}=-\sqrt{3}\Rightarrow {{u}_{M}}=-\sqrt{3}.{{u}_{P}}\Rightarrow {{v}_{M}}=-\sqrt{3}.{{v}_{P}}.\)
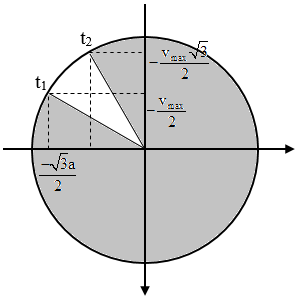
Ta có hình vẽ như bên.
Tại thời điểm t1, ta có:
\({{u}_{N}}=-{{A}_{M}}\Rightarrow {{u}_{M}}=-\frac{{{A}_{M}}\sqrt{3}}{2}\)
\(\Rightarrow {{v}_{M}}=-\frac{{{v}_{M\max }}}{2}=-60\text{ cm/s}\Rightarrow {{v}_{M\max }}=120\text{ cm/s}\text{.}\)
Tại thời điểm t2,
\({{v}_{M}}=-\frac{{{v}_{M\max }}.\sqrt{3}}{2}=-60\sqrt{3}\text{ cm/s}\Rightarrow {{\text{v}}_{P}}=\frac{-60\sqrt{3}}{-\sqrt{3}}=60\text{ cm/s}\text{.}\)











