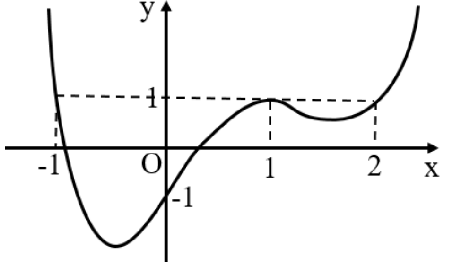
Cho hàm số bậc bốn f(x) có bảng biến thiên như sau
.png)
Số điểm cực trị của hàm số \(g(x) = {x^2}{\left[ {f(x + 1)} \right]^4}\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(g'(x) = 2x{\left[ {f(x + 1)} \right]^4} + 4{x^2}{\left[ {f(x + 1)} \right]^3}.f'(x + 1) = 2x{\left[ {f(x + 1)} \right]^3}.\left[ {f(x + 1) + 2x.f'(x + 1)} \right]\)
\(g'(x) = 0\) ta được
+ TH1: x = 0
+ TH2: \(f(x + 1) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a < – 2\\x = b \in ( – 2; – 1)\\x = c \in ( – 1;0)\\x = d > 0\end{array} \right.\)
+ TH3: \(f(x + 1) + 2x.f'(x + 1) = 0\).
Từ bảng biến thiên ta có hàm số thỏa mãn là \(f(x) = – 5{x^4} + 10{x^2} – 2\)
\( \Rightarrow f(x + 1) + 2x.f'(x + 1) = 0 \Leftrightarrow h\left( x \right) = f(x + 1) + 2(x + 1).f'(x + 1) – 2f'(x + 1) = 0\)
Với t = x + 1 ta có: \(h(t) = – 5{t^4} + 10{t^2} – 2 + 2t( – 20{t^3} + 20t) – 2( – 20{t^3} + 20t) = 0\)
\( \Leftrightarrow – 45{t^4} + 40{t^3} + 50{t^2} – 40t – 2 = 0\)
Lập bảng biến thiên ta suy ra có 4 nghiệm \(t \Rightarrow 4\) nghiệm x
Vậy có 9 cực trị.
.png)