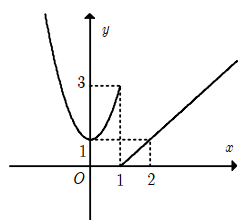
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x^{2}}{x} & \text { khi } x<1, x \neq 0 \\ 0 & \text { khi } x=0 \\ \sqrt{x} & \text { khi } x \geq 1 \end{array}\right.\). Hàm số f(x) liên tục tại:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\text { Hàm số } y=f(x) \text { có TXĐ: } \mathrm{D}=\mathbb{R} \text { . }\)
\(\text { Dễ thấy hàm số } y=f(x) \text { liên tục trên mỗi khoảng }(-\infty ; 0),(0 ; 1) \text { và }(1 ;+\infty) \text { . }\)
ta có \(\left\{ {\begin{array}{*{20}{l}} {f(0) = 0}\\ {\mathop {\lim }\limits_{x \to {0^ - }} f(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{{x^2}}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} x = 0}\\ {\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{{x^2}}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} x = 0} \end{array}} \right.\)\(\longrightarrow f(x) \text { liên tục tại } x=0\)
Lại có \(\left\{ {\begin{array}{*{20}{l}} {f(1) = 1}\\ {\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2}}}{x} = \mathop {\lim }\limits_{x \to {1^ - }} x = 1}\\ {\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \sqrt x = 1} \end{array}} \right.\)\(\longrightarrow f(x) \text { liên tục tại } x=1 \text { . }\)
\(\text { Vậy hàm số } y=f(x) \text { liên tục trên } \mathbb{R}\)
Câu hỏi liên quan
-
Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x^{3}-x^{2}+2 x-2}{x-1} & \text { khi } x \neq 1 \\ 3 x+m & \text { khi } x=1 \end{array} \text { liên tục tại } x=1\right.\)
-
Cho hàm số \(\begin{equation} f(x)=\frac{x^{2}+1}{x^{2}+5 x+6} \end{equation}\). Hàm số f (x) liên tục trên khoảng nào sau đây?
-
Cho hàm số \(f(x)=\left\{\begin{array}{cc} \frac{x^{2}-5 x+6}{2 x^{3}-16} & \text { khi } x<2 \\ 2-x & \text { khi } x \geq 2 \end{array}\right.\). Khẳng định nào sau đây đúng nhất.
-
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sqrt{x}-2}{x-4} & \text { khi } x \neq 4 \\ \frac{1}{4} & \text { khi } x=4 \end{array}\right.\). Khẳng định nào sau đây đúng?
-
Cho hàm số: \(f\left( x \right) = \frac{{\sqrt {x + 2} - \sqrt {2 - x} }}{x},x \ne 0\)
Phải bổ sung thêm giá trị f(0) bằng bao nhiêu để hàm số f(x) liên tục tại x = 0?
-
Cho hàm số \(f\left( x \right)\; = \left\{ {\begin{array}{*{20}{l}}
{\frac{{x + \sqrt {x + 2} }}{{x + 1}}\;\;khi\;x > \; - 1\;}\\
{2x + 3\;\;\;\;\;\;\;\;\;\;\;\;khi\;x\; \le - 1}
\end{array}} \right.\). Khẳng định nào sau đây đúng nhất. -
Xác định a, b để các hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {\,\sin x\,\,{\rm{khi }}\,\left| x \right| \le \frac{\pi }{2}}\\ {ax + b\,\,\,{\rm{khi}}\,\,\left| x \right| > \frac{\pi }{2}} \end{array}} \right.\) liên tục trên R.
-
Giá trị của \(\lim \frac{3 n^{3}+n}{n^{2}}\) bằng:
-
Tìm m để các hàm số \(f(x) = \left\{ \begin{array}{l} \frac{{\sqrt[3]{{x - 2}} + 2x - 1}}{{x - 1}}{\rm{ \ khi \ }}x \ne 1\\ 3m - 2{\rm{ \ khi \ }}x = 1 \end{array} \right.\) liên tục trên R.
-
Cho phương trình xsinx+x2−3=0. Nhận xét nào sau đây không đúng?
-
Biết rằng \(\lim\limits _{x \rightarrow 0} \frac{\sin x}{x}=1\). Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sin \pi x}{x-1} & \text { khi } x \neq 1 \\ m & \text { khi } x=1 \end{array} \text { liên tục tại } x=1\right. \text { . }\)
-
Cho hàm số \(f(x)=\left\{\begin{array}{ll} (x+1)^{2} & , x>1 \\ x^{2}+3 & , x<1 \\ k^{2} & , x=1 \end{array}\right.\). Tìm k để \(f(x)\) gián đoạn tại x=1
-
Hàm số y=f(x) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
-
Cho hàm số \(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2} - 3x + 2}}{{\sqrt {x - 1} }} + 2\;\;khi\;x\; > \;1}\\
{3{x^2} + x - 1\;\;\;\;\;\;\;\;\;\;khi\;x \le 1}
\end{array}} \right.\). Khẳng định nào sau đây đúng nhất -
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x^{2}-1}{x-1} & \text { khi } x<3, x \neq 1 \\ 4 & \text { khi } x=1 \\ \sqrt{x+1} & \text { khi } x \geq 3 \end{array}\right.\). Hàm số f(x) liên tục tại:
-
Số điểm gián đoạn của hàm số \(h(x)=\left\{\begin{array}{ll} 2 x & \text { khi } x<0 \\ x^{2}+1 & \text { khi } 0 \leq x \leq 2 \\ 3 x-1 & \text { khi } x>2 \end{array}\right.\)
-
Cho hàm số \( f(x) = \frac{{{x^2} + 1}}{{{x^2} + 5x + 6}}\). Hàm số f( x) liên tục trên khoảng nào sau đây?
-
Tìm a để hàm số \(f(x)=\left\{\begin{array}{l} \frac{\sqrt{3 x+1}-2}{x^{2}-1} \text { khi } x>1 \\ \frac{a\left(x^{2}-2\right)}{x-3} \quad \text { khi } x \leq 1 \end{array}\right.\) sau liên tục tại x=1.
-
Tìm a để hàm số \(f(x)=\left\{\begin{array}{l} \frac{\sqrt{4 x+1}-1}{a x^{2}+(2 a+1) x} \text { khi } x \neq 0 \\ 3 \quad \text { khi } x=0 \end{array}\right.\) liên tục tại x=0.
-
Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} x^{2} \sin \frac{1}{x} & \text { khi } x \neq 0 \\ m & \text { khi } x=0 \end{array}\right.\) liên
tục tại x = 0.
