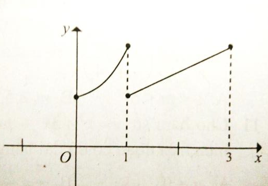Cho hàm số \(f(x)\). Hàm số \(y=f'(x)\) có đồ thị như hình sau.
Hàm số \(g(x)=3 f(1-2 x)+8 x^{3}-21 x^{2}+6 x\) đồng biến trên khoảng nào dưới đây?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(g^{\prime}(x)=-6 f^{\prime}(1-2 x)+24 x^{2}-42 x+6\)
\(g^{\prime}(x)<0 \Leftrightarrow f^{\prime}(1-2 x)<4 x^{2}-7 x+1(*)\)
Đặt \(1-2 x=t \Leftrightarrow x=\frac{1-t}{2}\)
Ta có (*) trở thành \(f^{\prime}(t)<4 \cdot\left(\frac{1-t}{2}\right)^{2}-7 \cdot \frac{1-t}{2}+1 \Leftrightarrow f^{\prime}(t)<t^{2}+\frac{3}{2} t-\frac{3}{2}\)
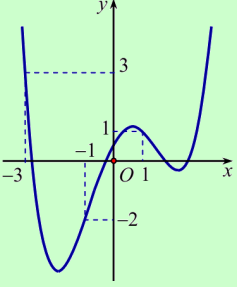
Ta vẽ parapol \((P): y=x^{2}+\frac{3}{2} x-\frac{3}{2}\) trên cùng hệ trục Oxy với đồ thị \(y=f^{\prime}(x)\) như hình vẽ sau, ta thấy (P) có đỉnh \(I\left(-\frac{3}{4} ;-\frac{33}{16}\right)\) và đi qua các điểm \((-3 ; 3),(-1 ;-2),(1 ; 1)\)
.png)
Từ đồ thị hàm số ta thấy trên khoảng (- 3;1) ta có \(f^{\prime}(t)<t^{2}+\frac{3}{2} t-\frac{3}{2} \Leftrightarrow-3<t<-1\)
\(\Leftrightarrow-3<1-2 x<-1 \Leftrightarrow 1<x<2\)
Vậy hàm số g(x) nghịch biến trên khoảng (1;2).
Câu hỏi liên quan
-
Hàm số \(y = \frac{1}{3}{x^3} + {x^2} - x\) đồng biến trên các khoảng:
-
Hàm số \(y = {x^3} - 2{x^2} + x - 1\) đồng biến trên khoảng nào sau đây?
-
Cho hàm số \(y = {x^3}--{x^2} + \left( {m - 1} \right)x + m.\). Tìm điều kiện của tham số m để hàm số đồng biến trên R
-
Hàm số \(y = {x^3} - 2{x^2} + x - 1\) nghịch biến trên các khoảng:
-
Cho hàm số \(y=f(x)\). Hàm số\(y=f'(x)\) có đồ thị như hình vẽ bên. Hàm số \(y=f\left(x^{2}-2\right)\) đồng biến trên khoảng
.png)
-
Trong các hàm số sau, hàm số nào nghịch biến trên các khoảng xác định của chúng
-
Cho hàm số y = \({x^3}\; + \;3{x^2}\; - \;3x\; + \;2\). Khẳng định nào sau đây là khẳng định đúng?
-
Cho hàm số \(y = \frac{{mx + 4m}}{{x + m}}\) với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S.
-
Hàm số \(y = {x^3} - 5{x^2} + 5\) nghịch biến trên khoảng nào sau đây?
-
Tìm khoảng đồng biến của hàm số \(y= 4x ³ - x ² - 4x -2\)
-
Cho hàm \(y = \sqrt {{x^2} – 6x + 5} \). Mệnh đề nào sau đây là đúng?
-
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(\sqrt {{x^2} + mx + 2} = 2x + 1\) có hai nghiệm thực?
-
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}( x)=x^{2} (1-4 x^{2}), \quad \forall x \in \mathbb{R}\) . Hàm số y=f(cos x) đồng biến trên khoảng nào dưới đây?
-
Hàm số \(y = {x^2} + 2x\) nghịch biến trên các khoảng:
-
Hàm số y = x4 – 2x2 + 3 đồng biến trên các khoảng nào?
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y=f(x)=x+m \cos x\) luôn đồng biến trên \(\mathbb{R}\) ?
-
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) có f (0)=0 và đồ thị hàm số y=f'(x)như hình vẽ dưới đây
Hàm số \(y=\left|3 f(x)-x^{3}\right|\)3 đồng biến trên khoảng:
-
Cho hàm số \(y\; = \;\sqrt {3{x^2}\; - \;{x^3}} \). Khẳng định nào sau đây là khẳng định sai?
-
Tìm m để hàm số \(y=\frac{x-m}{x+1}\) đồng biến trên từng khoảng xác định của chúng.
-
Có bao nhiêu giá trị nguyên của tham số m thuộc (-2020;2020) để hàm số \(y=\frac{\sin x-3}{\sin x-m}\) đồng biến trên \(\left(0 ; \frac{\pi}{4}\right)\).
