Cho hàm số \(f(x)=x^{3}-m x^{2}-(m-6) x+1\) . Có bao nhiêu số nguyên dương m để hàm số\(y=f(x+\sqrt{x^{2}+1})\) đồng biến trên khoảng \((-\infty ;+\infty)\).
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiYêu cầu bài toán \(\Leftrightarrow y^{\prime}=\left(1+\frac{x}{\sqrt{x^{2}+1}}\right) f^{\prime}(x+\sqrt{x^{2}+1}) \geq 0, \forall x \Leftrightarrow f^{\prime}(x+\sqrt{x^{2}+1}) \geq 0, \forall x(1)\)
Đặt \(t=x+\sqrt{x^{2}+1} \in(0 ;+\infty), \forall x \text { và } f^{\prime}(x)=3 x^{2}-2 m x+6-m\)
Do vậy \((1) \Leftrightarrow f^{\prime}(t) \geq 0, \forall t \in(0 ;+\infty) \Leftrightarrow 3 t^{2}-2 m t+6-m \geq 0, \forall t \in(0 ;+\infty)\)
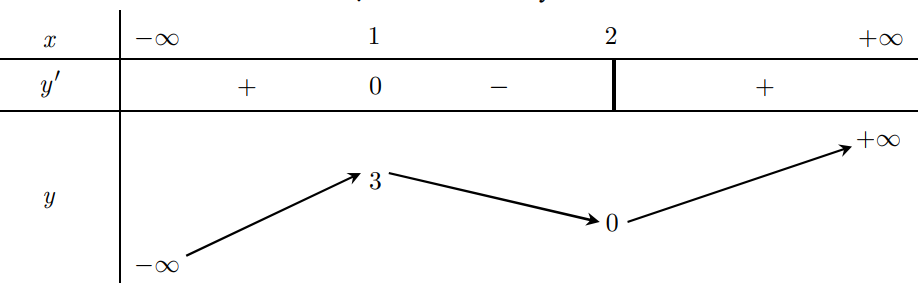
\(\Leftrightarrow m \leq \frac{3 t^{2}+6}{2 t+1}, \forall t \in(0 ;+\infty) \quad m \leq \min _{[0 ;+\infty)}\left\{y=\frac{3 t^{2}+6}{2 t+1}\right\}=y(1)=3 \Rightarrow m \in\{1,2,3\}\)
Vậy có 3 giá trị m cần tìm.
.png)











