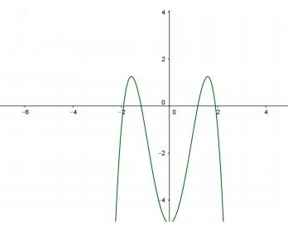
Cho hàm số \(y = {x^3} – 3{x^2} + 4\) có đồ thị \(\left( C \right)\). Gọi d là đường thẳng qua \(I\left( {1;2} \right)\) với hệ số góc k. Tập tất cả các giá trị của k để d cắt \(\left( C \right)\) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương trình \(d:y = k\left( {x – 1} \right) + 2\).
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
\({x^3} – 3{x^2} + 4 = kx – k + 2 \Leftrightarrow {x^3} – 3{x^2} – kx + k + 2 = 0\,\,\,\,\,\left( 1 \right)\)
\( \Leftrightarrow \left( {x – 1} \right)\left( {{x^2} – 2x – k – 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\\underbrace {{x^2} – 2x – k – 2}_{g(x)} = 0\;\;(*)\end{array} \right.\)
d cắt \(\left( C \right)\) tại ba điểm phân biệt \( \Leftrightarrow \) Phương trình (*) có hai nghiệm phân biệt \({x_1};{x_2}\) khác 1
\( \Leftrightarrow \left\{ \begin{gathered}{{\Delta ‘}_g} > 0 \hfill \\g\left( 1 \right) \ne 0 \hfill \\\end{gathered} \right.\)
\( \Leftrightarrow \left\{ \begin{gathered} k + 3 > 0 \hfill \\ – 3 – k \ne 0 \hfill \\ \end{gathered} \right. \Leftrightarrow k > – 3\)
Hơn nữa theo Viet ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2 = 2{x_I}\\{y_1} + {y_2} = k\left( {{x_1} + {x_2}} \right) – 2k + 4 = 4 = 2{y_I}\end{array} \right.\) nên I là trung điểm AB.
Vậy chọn k > – 3, hay \(\left( { – 3; + \infty } \right)\).
.png)
.png)