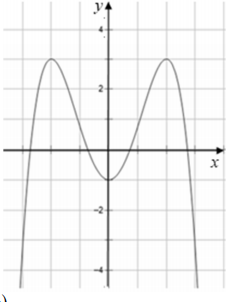
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình \(m \cdot 4^{x}+(m-1) \cdot 2^{x+2}+m-1>0\) nghiệm đúng \(\forall x \in \mathbb{R} ?\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=2^{x}>0 \text { thì } m \cdot 4^{x}+(m-1) \cdot 2^{x+2}+m-1>0, \text { đúng } \forall x \in \mathbb{R}\)
\(\begin{array}{l} \Leftrightarrow m \cdot t^{2}+4(m-1) \cdot t+(m-1)>0, \forall t>0 \Leftrightarrow m\left(t^{2}+4 t+1\right)>4 t+1, \forall t>0 \\ \Leftrightarrow g(t)=\frac{4 t+1}{t^{2}+4 t+1}<m, \forall t>0 \end{array}\)
Ta có \(g^{\prime}(t)=\frac{-4 t^{2}-2 t}{\left(t^{2}+4 t+1\right)^{2}}<0\) nên g(t) nghịch biến trên \([0 ;+\infty)\)
\(\mathrm{ycbt} \Leftrightarrow \max \limits_{t \geq 0} g(t)=g(0)=1 \leq m\)
Câu hỏi liên quan
-
Cho hàm số y = f(x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị hàm số y = f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ?
-
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\)và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=f(|x|)?
.png)
-
Với mọi m ∈ (-1; 1) phương trình \({\sin ^2}x + \cos x = m\) có mấy nghiệm trên đoạn [0; π] ?
-
Bảng biến thiên sau là của hàm số nào?
-
Đường thẳng y=m không cắt đồ thị hàm số \(y=-2 x^{4}+4 x^{2}+2\) thì tất cả các giá trị tham số m là
-
Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số \(y\; = \;\frac{x}{{\left| {x\; - \;1} \right|}}\) ?
-
Cho hàm số \(y=2{x^3} - 3\left( {m + 1} \right){x^2} + 6\left( {m + 1} \right)2x + 1\). Hình nào dưới đây mô tả chính xác nhất đồ thị hàm số trên?
-
Cho hàm số y=f(x) liên tục trên đoạn [-2;2] và có đồ thị là đường cong như trong hình vẽ bên.
Hỏi phương trình \(|f(x)-1|=2\) có mấy nghiệm phân biệt trên [-2;2]? -
Tính tổng các hoành độ của những điểm thuộc đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGdbaacaGLOaGaayzkaaGaaiOoaiaadMhacqGH9aqpcaWG4bWaaWba % aSqabeaacaaIZaaaaOGaeyOeI0IaaG4maiaadIhadaahaaWcbeqaai % aaikdaaaGccqGHRaWkcaaIYaaaaa!4230! \left( C \right):y = {x^3} - 3{x^2} + 2\) cách đều hai điểm A(12;1),B(-6;3) .
-
Tất cả giá trị của tham số m để phương trình \({x^4} – 2{x^2} – m + 3 = 0\) có bốn nghiệm phân biệt là
-
Đồ thị sau đây là của hàm số nào?
-
Đồ thị sau đây là của hàm số nào?
-
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\backslash{\{1\}}\) và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=f(x+1)?
-
Cho hàm số y = x4 – 4x2 – 2 có đồ thị (C) và đồ thị (P) : y = 1- x2. Số giao điểm của (P) và đồ thị (C) là
-
Bảng biến thiên dưới đây là bảng biến thiên của hàm số nào trong các hàm số được liệt kê ở bốn phương án A, B, C, D?
-
Hàm số y = f(x) xác định, liên tục trên khoảng K và có đạo hàm f′(x) trên K. Biết hình vẽ sau đây là của đồ thị hàm số f′(x) trên K.
.png)
Khẳng định nào sau đây là đúng?
-
Cho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) có đồ thị (C) và đường thẳng d: y = x + m. Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A, B sao cho \(AB = \sqrt {10} \) là
-
Cho hàm số y = f(x) có đạo hàm trên (a;b) . Phát biểu nào sau đây là đúng ?
-
Cho hàm số y = x3 + ax2 + bx + c đi qua điểm A(0;-4) và đạt cực đại tại điểm B(1;0) hệ số góc k của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng -1 là:
-
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với a > 0 có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
