Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(2 \sqrt{x+1}=x+m\) có nghiệm thực?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiĐặt \(t=\sqrt{x+1}, t \geq 0\)
Phương trình trở thành \(2 t=t^{2}-1+m \Leftrightarrow m=-t^{2}+2 t+1\)
Xét hàm số \(f(t)=-t^{2}+2 t+1, t \geq 0 ; f^{\prime}(t)=-2 t+2\)
Bảng biến thiên hàm số f(t)
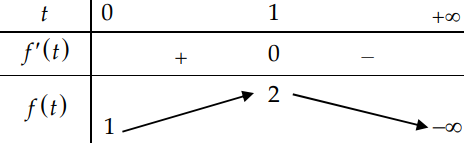
Từ đó suy ra phương trình có nghiệm khi \(m \leq 2\)
ADMICRO
YOMEDIA
ZUNIA9