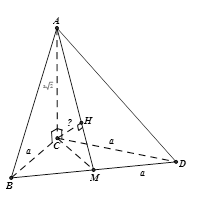
Cho hình chóp A.BCD có cạnh AC vuông góc (BCD) và BCD là tam giác đều cạnh bằng a. Biết \(AC = a\sqrt 2\) và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiDựng \(CH⊥AM⇒d(C,AM)=CH\)
Vì ΔBCD là tam giác đều cạnh a và M là trung điểm của BD nên dễ tính được \( CM = \frac{{a\sqrt 3 }}{2}\)
Xét ΔACM vuông tại C có CH là đường cao, ta có:
\(\begin{array}{*{20}{l}} {\frac{1}{{C{H^2}}} = \frac{1}{{C{A^2}}} + \frac{1}{{C{M^2}}} = \frac{1}{{2{a^2}}} + \frac{1}{{\frac{{3{a^2}}}{4}}} = \frac{{11}}{{6{a^2}}}}\\ { \Rightarrow C{H^2} = \frac{{6{a^2}}}{{11}} \Rightarrow CH = a\sqrt {\frac{6}{{11}}} } \end{array}\)
ADMICRO
YOMEDIA
ZUNIA9